正規性の検定

正規性を確認せずに検定を選択しちゃダメなの?

正規性を確認せずに,正規分布でないデータにパラメトリック検定を適応したり,正規分布のデータにノンパラメトリック検定を適応してしまうと,正しい結果が得られません!
正規性分布ってどうやって判断するの?
正規性(データが正規分布しているかどうか)を判断するためにはいくつかの方法が存在します.
- ヒストグラムを確認する
- 正規確率プロットを確認する
- 正規性の検定を行う

ヒストグラムから正規性を判断しちゃだめなの?

ヒストグラムからの正規性の判断には限界があります!
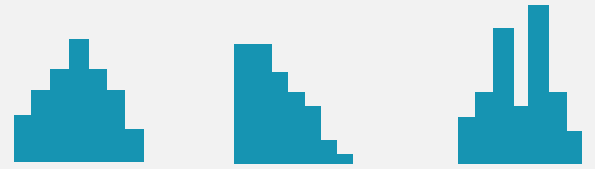
例えばヒストグラムを作成した際に左側のような分布になれば誰も正規分布だといった結論に反対する方はいないと思います.
また中央のような分布になれば,これも正規分布ではないと判断する方がほとんどでしょう.
ただ右側のような分布になった場合にはいかがでしょうか?
これは正規分布と判断するか非正規分布と判断するか非常に難しいところだと思います.
このようにヒストグラムによる正規性の判断というのは主観的な判断にすぎません.
またサンプルサイズが小さい場合にはヒストグラムを使って正規性を判断することが困難な場合が多いです.
2の正規確率プロットを用いた正規性の検定も,最終的には散布図からプロットしたデータの直線性を確認するものですが,これもやはり主観的な判断に終わってしまいます.
そこで最も勧められる方法が正規性の検定(Shapiro-wilk(シャピロウィルク)検定)というわけです.
正規性の検定が実施できる統計ソフト

正規性の検定ができる統計ソフトってどんなのがありますか?

正規性の検定ができる統計ソフトって実は少ないんですよね
エクセルで簡易的に正規性の検定ができればよいのですが,実は正規性の検定が搭載されている統計ソフトというのは比較的少ないのです.
例えばすぐできるリハビリテーション統計に付属しているJ-STATなんかは正規性の検定が搭載されていないことで有名です.
SPSS,R(EZR),エクセル統計なんかが正規性の検定が搭載されている統計ソフトとしては有名でしょうか.
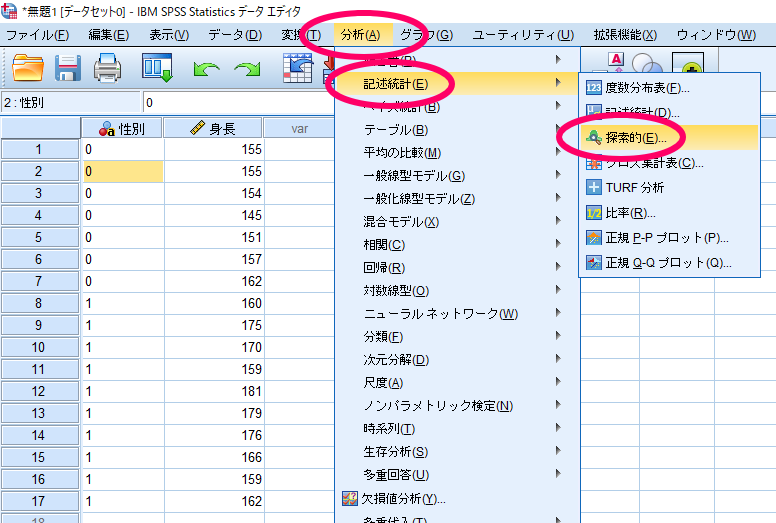
SPSSによる正規性の検定の方法(1標本の場合)
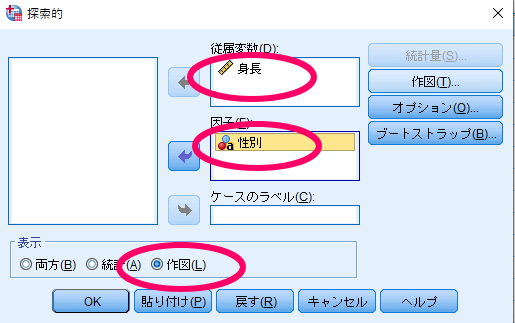
ここでは1標本を想定して性別(0=女性)と身長のデータを例にSPSSを使用した正規性の検定の方法をお示しいたします.
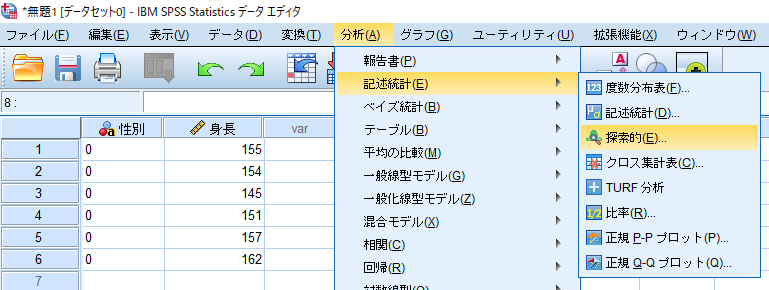
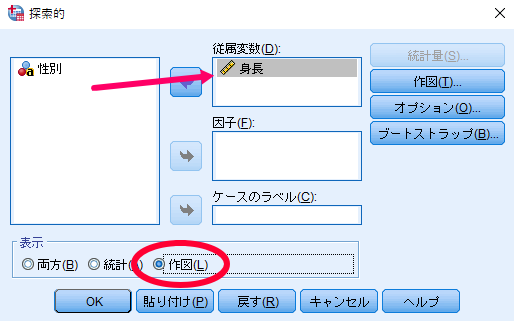
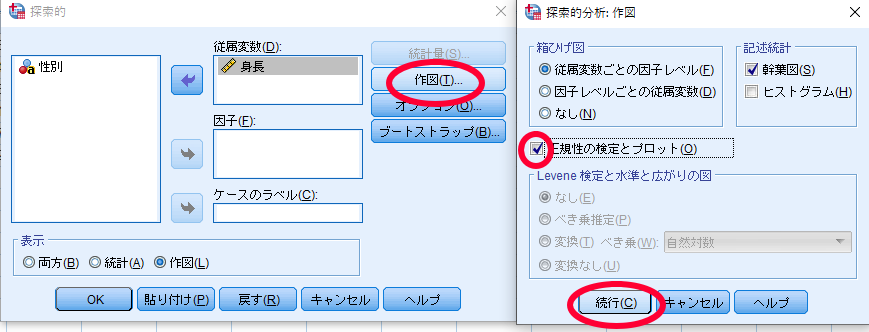
これで数秒待てば結果が出力されます.
SPSSによる正規性の検定の確認方法・結果の見方(1標本の場合)
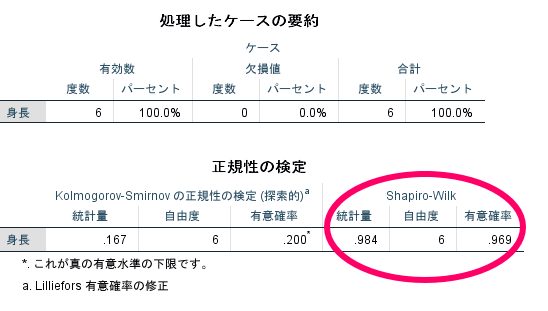
このように結果にはいろいろな情報が表示されますが,基本的にはShapiro-Wilk検定の部分の有意確率を参照すればよいだけです.
ちなみにShapiro-Wilk検定の左横にKolmogorov-Sminornov検定の結果も表記されますが無視して問題ありません.
結果の判断の方法ですが,
有意確率(p)<0.05:正規分布に従わない
有意確率(p)≧0.05:正規分布に従う(厳密にいえば正規分布に従わないとは言えない)
となります.
この場合には,p=0.969で有意確率が5%を上回っておりますので,正規分布に従う(厳密にいえば正規分布に従わないとは言えない)と解釈できます.
したがってこの場合には,パラメトリック検定を使用することとなります.
SPSSによる正規性の検定の方法(2標本の場合)
ここでは1標本を想定して性別(0=女性,1=男性)と身長のデータを例にSPSSを使用した正規性の検定の方法をお示しいたします.
例えば男性と女性の身長を比較したいといった場合に,2群間の比較検定を行う前にまずはデータの正規性を確認して,対応の無いt検定を用いるか,Mann-WhitneyのU検定を用いるかを判断することになります.

1標本と2標本って何が違うの?

2標本の場合には,グループ毎(ここでは性別毎)に正規性を判断する必要があります.つまり男性のデータの正規性と,女性のデータの正規性を別々に判定する必要があるわけです.
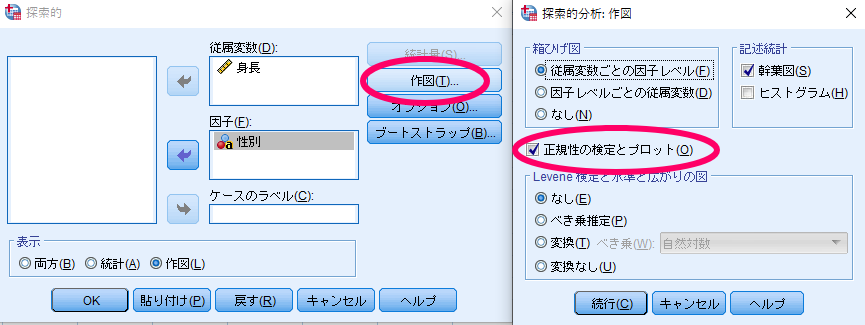
SPSSによる正規性の検定の確認方法・結果の見方(2標本の場合)
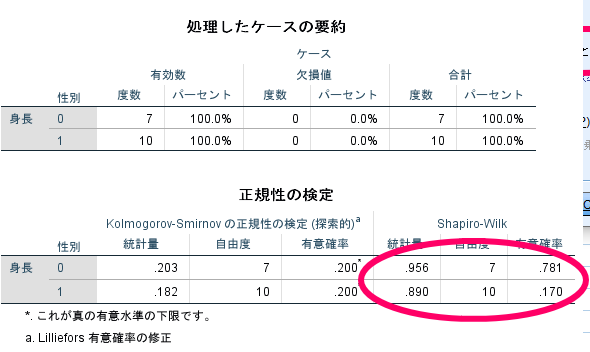
このように結果にはいろいろな情報が表示されますが,基本的にはShapiro-Wilk検定の部分の有意確率を参照すればよいだけです.
2標本の場合には,性別毎に有意確率を見ていく必要があります.
結果の判断の方法も1標本の場合と同様です.
有意確率(p)<0.05:正規分布に従わない
有意確率(p)≧0.05:正規分布に従う(厳密にいえば正規分布に従わないとは言えない)
標本の場合には,男性・女性それぞれの有意確率を確認する必要があります.
この場合には,女性でp=0.781で,男性でp=0.170ですので,男性・女性ともに有意確率が5%を上回っておりますので,男性・女性ともに正規分布に従う(厳密にいえば正規分布に従わないとは言えない)と解釈できます.
したがってこの場合には,パラメトリック検定を使用することとなります.




コメント
[…] ・正規分布に従うデータであること(正規性の判断についてはコチラを参照) […]
[…] ・正規分布に従うデータ(正規性の判断についてはコチラを参照してください) […]
[…] ・正規分布に従うデータ(正規性の判断についてはコチラを参照してください) […]
[…] ・正規分布以外の分布に従うデータ(正規性の判断についてはコチラを参照してください) […]
[…] ・正規分布以外の分布に従うデータ(正規性の判断についてはコチラを参照してください) […]
[…] ・正規分布に従うデータ(正規性の判断についてはコチラを参照してください) […]
[…] ・正規分布以外の分布に従うデータ(正規性の判断についてはコチラを参照してください) […]
[…] ・正規分布に従うデータ(正規性の判断についてはコチラを参照してください) […]
[…] ・正規分布に従うデータ(正規性の判断についてはコチラを参照してください) […]
[…] ・正規分布以外に従うデータ(正規性の判断についてはコチラを参照してください) […]
[…] SPSSによる正規性の検定Shapiro-wilk(シャピロウィルク)検定今回は統計ソフトS… […]
[…] SPSSによる正規性の検定Shapiro-wilk(シャピロウィルク)検定 […]