- ノンパラメトリック検定であるMann-Whitney(マンホイットニー)のU検定の適用の条件
- SPSSを使用したMann-Whitney(マンホイットニー)のU検定-データ入力の方法に注意-
- SPSSを使用したMann-Whitney(マンホイットニー)のU検定の方法 その①
- SPSSを使用したMann-Whitney(マンホイットニー)のU検定の結果の見方・確認方法 その①
- SPSSを使用したMann-Whitney(マンホイットニー)のU検定の方法 その②
- SPSSを使用したMann-Whitney(マンホイットニー)のU検定の結果の見方・確認方法 その②
- SPSSを用いてMann-Whitney(マンホイットニー)のU検定を行った際のグラフ作成
- Mann-Whitney(マンホイットニー)のU検定における効果量(r)の算出
ノンパラメトリック検定であるMann-Whitney(マンホイットニー)のU検定の適用の条件
Mann-Whitney(マンホイットニー)のU検定を適用するためにはいくつかの条件を満たす必要があります.
ここではまずMann-Whitney(マンホイットニー)のU検定を適用するための4つの条件をお示しいたします.
・正規分布以外の分布に従うデータ(正規性の判断についてはコチラを参照してください)
・データが比率尺度データ・間隔尺度データ・順序尺度のデータ
・中央値を比較することが意味を持つデータ
・2つの標本を対象としたデータ
(3つ以上になると異なる検定を使用する必要があります)

対応がないって何?

対応がないというのは比べるデータが同一対象例のデータではないことを意味します
ここで重要なのは対応のないt検定(2標本t検定)というのは2つの標本に対して用いられる検定であるといった点です.
例えば男性と女性で体重を比較するとか,高齢者と若年者で握力を比較するといったような場合には,異なる対象例のデータを比較することとなります.
このように異なる対象例の2つのデータを比較する場合には対応のないt検定(2標本検定)を用いることとなります.
2つの対応のデータを比較する検定には,パラメトリックの検定である対応のないt検定(2標本t検定)と,ノンパラメトリックの検定であるMann-Whitney(マンホイットニー)のU検定が存在します.
順序尺度データの場合や,間隔尺度データ・比率尺度データであってもデータの正規性が確認できない場合には,Mann-Whitney(マンホイットニー)のU検定を使用することとなります.
SPSSを使用したMann-Whitney(マンホイットニー)のU検定-データ入力の方法に注意-
SPSSでMann-Whitney(マンホイットニー)のU検定を行う場合にはデータの入力方法に注意が必要です.
実はパラメトリック検定であってもノンパラメトリック検定であっても,対応のある検定と対応の無い検定ではデータの並べ方も異なるものとなります.
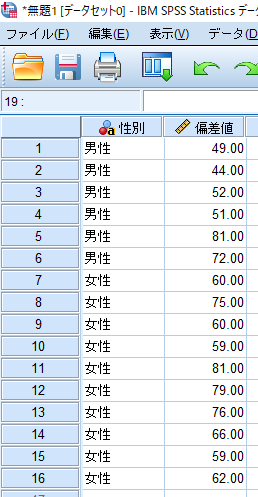
対応の無い検定の場合には,測定データ(偏差値)を縦列に並べ,その横にグループを表すデータ(性別等:男性=0,女性=1)を入力します.
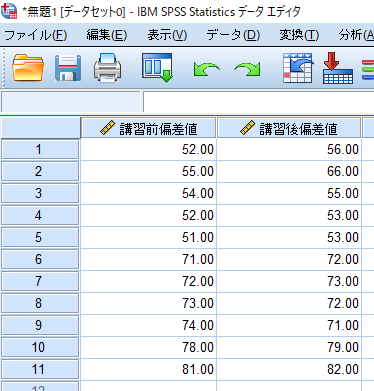
対応のある検定の場合には,このように横列に同一対象者のデータ(某予備校の全国模試の偏差値)を並べます.
SPSSを使用したMann-Whitney(マンホイットニー)のU検定の方法 その①
実はノンパラメトリック検定には2つほど方法があります.
旧バージョンを使用された経験のある方は後でご紹介する2つ目の方法の方がなじみがあるかもしれませんね.
まずは1つ目の方法についてご説明いたします.
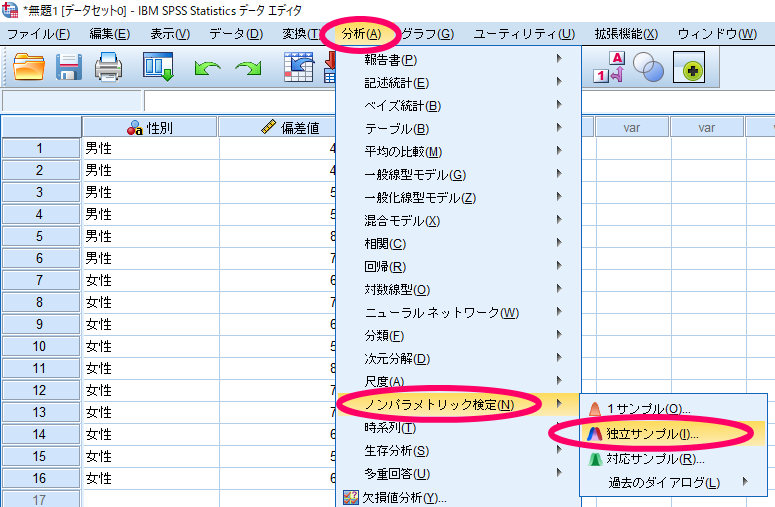
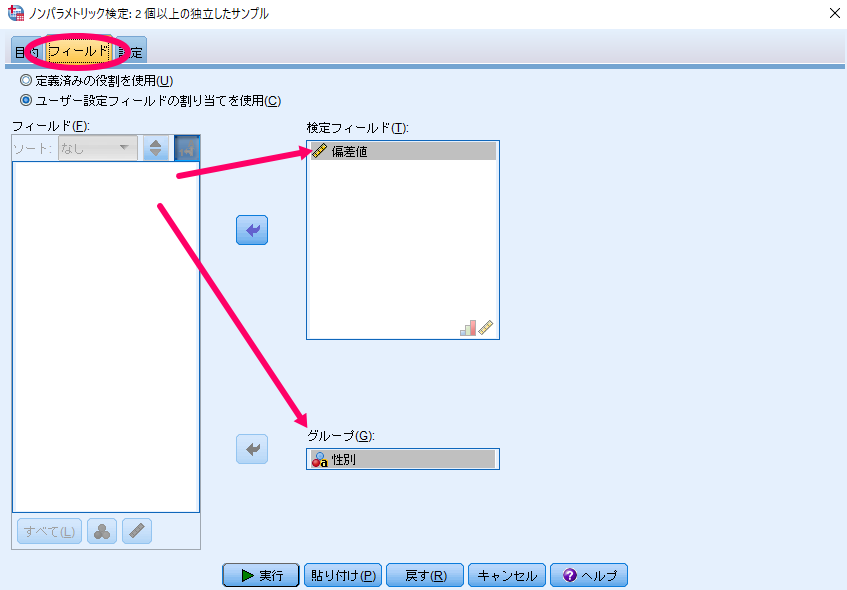
設定タブで有意水準を設定することができますが,基本的にはデフォルトの5%の設定で問題なければ操作する必要はありません.
このまま実行を押せば完了です.
SPSSを使用したMann-Whitney(マンホイットニー)のU検定の結果の見方・確認方法 その①

これがMann-Whitney(マンホイットニー)のU検定の結果です.
この画面では有意確率しか表示されませんので,この表をダブルクリックすると以下のような出力が表示されます.
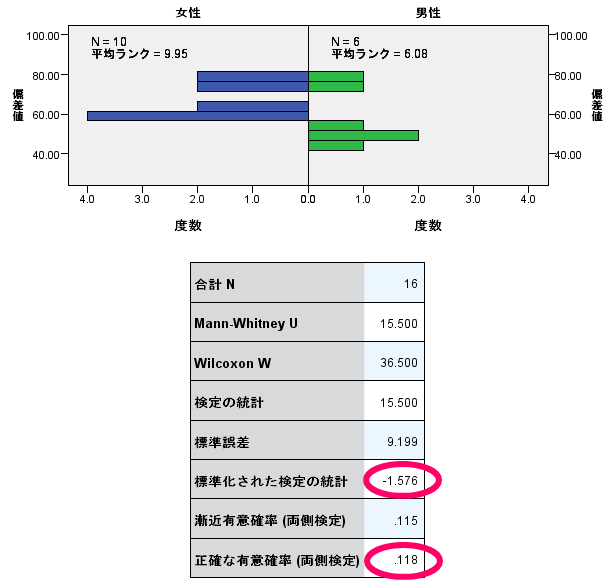
この有意確率を見れば,男性と女性で偏差値に変化があったのかどうかがわかります.
有意確率(p)<0.05:差がある
有意確率(p)≧0.05:差がない(厳密にいえばあるともないとも言えない)
この場合には,有意確率が0.118で5%以上ですので,男女で偏差値に有意な差がない(厳密にはあるともないともいえない)といった解釈ができます.
合わせて標準化された検定の統計量(Z)=-1.576を確認しておくと良いでしょう.
この統計量(Z)を用いることで効果量を算出できます.
効果量については後述いたします.
この方法ではMann-Whitney(マンホイットニー)のU検定で必須の中央値や四分位が出力されませんので,後述いたします2つ目の方法で解析を行うことが勧められます.
SPSSを使用したMann-Whitney(マンホイットニー)のU検定の方法 その②
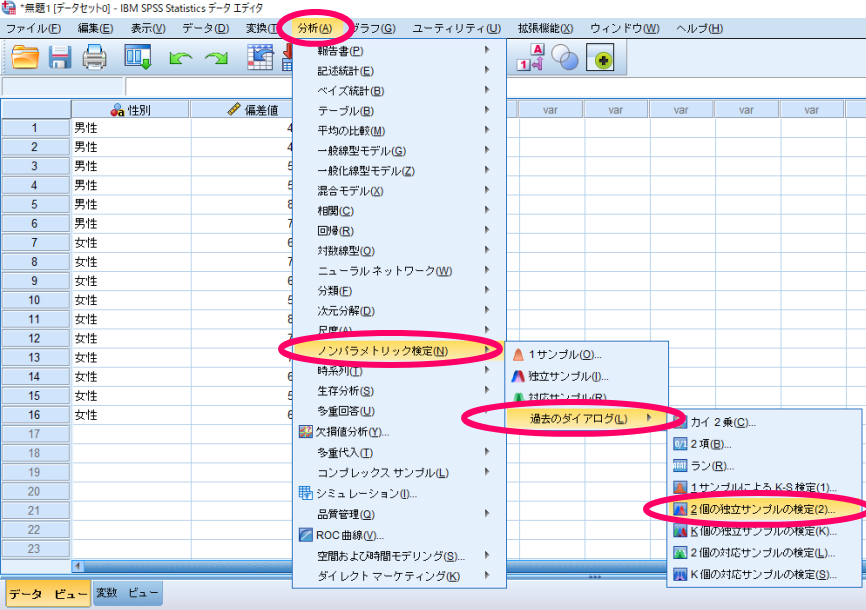
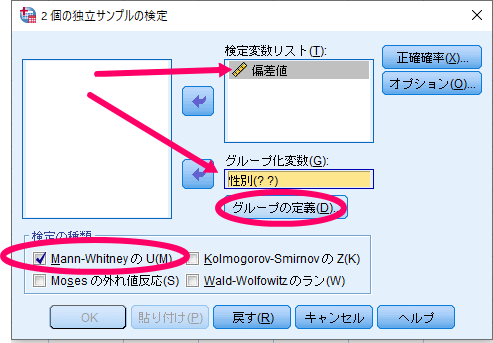
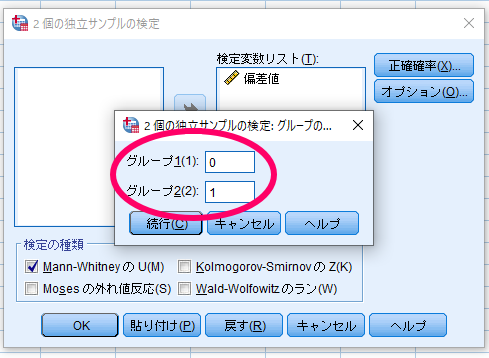
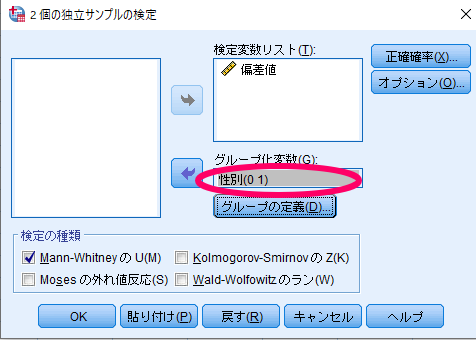
最終的にグループ化変数が性別(??)から性別(0 1)といった表記に変化することを確認します.
最後にオプションをクリックしてオプション設定を行います.
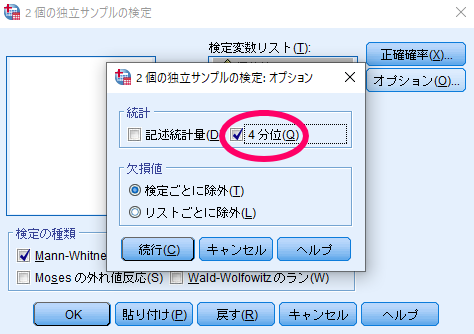
これで完了です.
SPSSを使用したMann-Whitney(マンホイットニー)のU検定の結果の見方・確認方法 その②
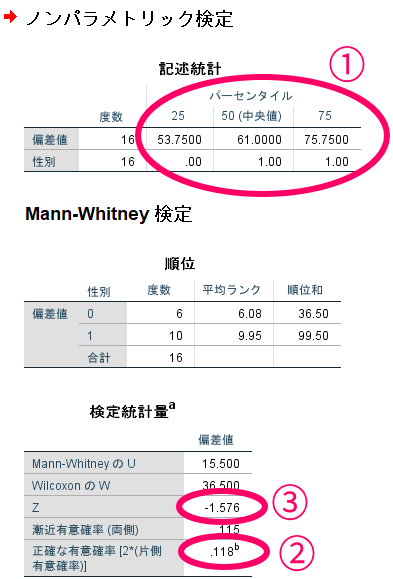
これがMann-Whitney(マンホイットニー)のU検定の結果です.
この表を見れば,全対象例の第1四分位・中央値・第3四分位を読み取ることができます.
別に新たに中央値や四分位を算出する必要がありませんのでこの方法がお勧めです.
この有意確率を見れば,最終的に講習前後で偏差値に変化があったのかどうかがわかります.
有意確率(p)<0.05:差がある
有意確率(p)≧0.05:差がない(厳密にいえばあるともないとも言えない)
この場合には,有意確率が0.118で5%以上ですので,前後で有意な差がない(厳密にはあるともないともいえない)といった解釈ができます.
検定の統計と表記されているものが統計量(Z)です.
素人が理解しておく必要はあまりないものですが,効果量を算出する上ではこの統計量(Z)が必要となります.
効果量についてはまた後でご紹介させていただきますので,ここでは効果量を算出するために必要な数値であるくらいの認識で良いと思います.
SPSSを用いてMann-Whitney(マンホイットニー)のU検定を行った際のグラフ作成
Mann-Whitney(マンホイットニー)のU検定を用いる場合にはデータに正規性が無いことが前提となりますので,Mann-Whitney(マンホイットニー)のU検定を用いた場合に使用すべきグラフは中央値と四分位を用いた箱ひげ図です.
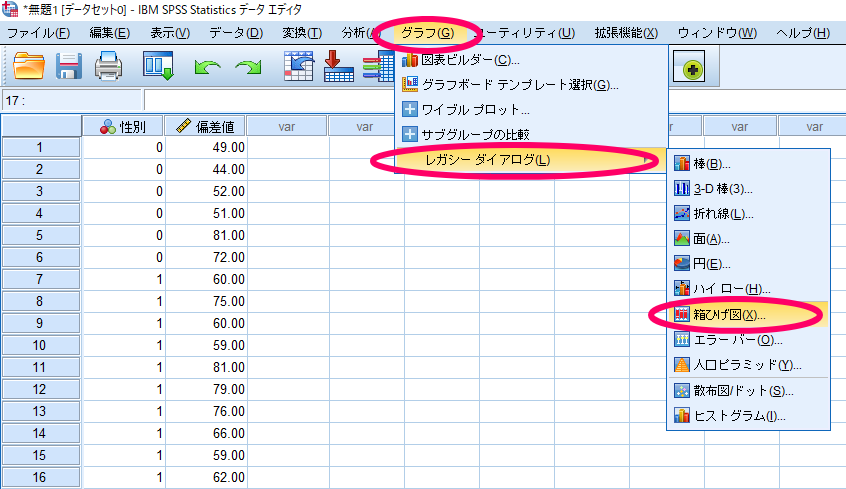
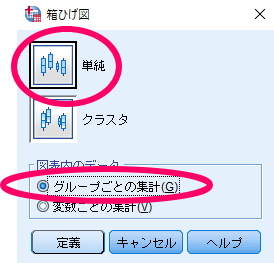
ここで重要なのは対応のないデータの場合には,図表内のデータで「グループごとの集計」を選択する点です.
ちなみに対応のあるデータを用いて箱ひげ図を作成する場合には,図表内のデータで「変数ごとの集計」を選択する必要があります.
最後に「定義」をクリックします.
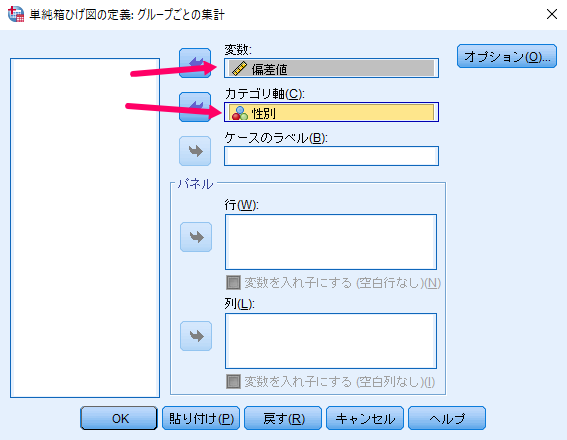
オプションは特に設定する必要はありません.

これが完成した箱ひげです.
箱の上端が第3四分位,箱の中の横線が中央値,箱の下端が第1四分位を表しております.
Mann-Whitney(マンホイットニー)のU検定における効果量(r)の算出
最近は対応のあるt検定を行った場合には,有意確率・95%信頼区間と合わせて効果量(rやd)を算出するのが一般的になってきております.
はじめにSPSSでは効果量を算出することはできませんので,先ほどお示しいたしました自由度やt値といった統計量を使用して効果量を算出することになります.

ところで効果量って何?

効果量というのはデータの単位に依存しない標準化された効果の程度を表す指標です.
先ほど男女間における偏差値の変化の差をMann-Whitney(マンホイットニー)のU検定を用いて比較しました.
例えばある研究では講習による学習を偏差値を用いて検討を行っていたのに対して,ある研究では講習による学習効果を,テストの点数そのものをアウトカムとして検討を行っていたとします.
この場合にはアウトカムの単位が異なりますので2つの研究の間でどちらが効果があったのかを単純比較することができません.
このように単位の異なる研究から得られた効果の比較や人数の異なる研究から得られた効果を比較する際に役立つのが効果量という指標です.
ノンパラメトリック検定の場合にはrという効果量が用いられるのが一般的です.

効果量ってどうやって算出するの?

効果量の算出には以下のエクセルファイルがとても便利です.
ここではこのエクセルファイルを用いて効果量(r)を算出いたしました.

先ほどのSPSSを用いて行ったMann-Whitney(マンホイットニー)のU検定の結果で得られた統計量(Z)=-1.576と人数=16を上記のエクセルファイルに打ち込むと簡単に効果量が算出できます.
この場合には効果量(r)=0.39で効果量中と判定されました.
今回はそもそも有意差が無かったわけですが,有意差が無いにもかかわらず効果量が大きい場合にはもう少しサンプルサイズを増やすと差が出る可能性が高いです.
一方で有意差が無い場合に効果量が小さい場合にはサンプルサイズを増やしても差が出る可能性は低いと考えることができます.

効果量の大きさってどうやって判断するの?

あくまで目安ですが下の表が非常に参考になります.効果量(r)の場合は,相関係数をイメージすると理解しやすいでしょうね.

http://jspt.japanpt.or.jp/ebpt_glossary/effect-size.htmlより引用



コメント
[…] Mann-WhitneyのU検定やWilcoxonの符号付順位検定ではZ値と呼ばれる統計量を使用して,有意かどうかを判断します. […]