- ノンパラメトリック検定であるスピアマン(Spearman)の順位相関係数の適用の条件
- SPSSを使用したスピアマン(Spearman)の順位相関係数-データ入力の方法-
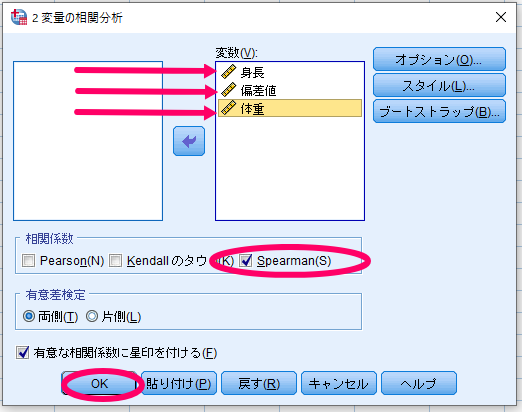
- SPSSを使用したスピアマン(Spearman)の順位相関係数-2変数の関連性を明かにしたい場合-
- SPSSを使用したスピアマン(Spearman)の順位相関係数の結果の見方・確認方法 -2変数の関連性を明かにしたい場合-
- SPSSを使用したスピアマン(Spearman)の順位相関係数の算出方法-相関行列を作成して3変数以上の関連性を明かにしたい場合-
- SPSSを使用したスピアマン(Spearman)の順位相関係数の結果の見方・確認方法 -3変数以上の関連性を明かにしたい場合-
- SPSSを用いてスピアマン(Spearman)の順位相関係数を行った際のグラフ作成
- Spearman(スピアマン)の順位相関係数における効果量(r)の算出
ノンパラメトリック検定であるスピアマン(Spearman)の順位相関係数の適用の条件
スピアマン(Spearman)の順位相関係数を算出する場合には,いくつかの条件を満たす必要があります.
ここではノンパラメトリックの検定であるスピアマン(Spearman)の順位相関係数を適用するための3つの条件をお示しいたします.

対応があるって何?

対応があるというのは関係性を調査するデータが同一対象例のデータであることを意味します
例えばある集団における身長と偏差値の関係性を明かにする場合に相関分析が用いられます.
2つのデータの関係性を分析する検定には,パラメトリックの検定であるPearson(ピアソン)の積率相関係数と,ノンパラメトリックの検定であるSpearman(スピアマン)の順位相関係数が存在します.
2変数がともに間隔尺度データ・比率尺度データであってデータに正規性が確認できる場合にはPearson(ピアソン)の積率相関係数を用います.
2変数のうち1変数が順序尺度データ(多段階のものは除く)の場合や,1変数が間隔尺度データ・比率尺度データであってもデータの正規性が確認できない場合には,Spearman(スピアマン)の順位相関係数を使用することとなります.
ちなみに2変数ともに順序尺度データ(多段階のものは除く)の場合や,2変数がともに間隔尺度データ・比率尺度データであってデータの正規性が確認できない場合にも,Spearman(スピアマン)の順位相関係数を使用することとなります.
2変数ともに正規分布の間隔・比率尺度データ
⇒ Pearson(ピアソン)の積率相関係数
1変数が順序尺度または非正規分布の間隔・比率尺度データ
⇒ Spearman(スピアマン)の順位相関係数
2変数ともに順序尺度または非正規分布の間隔・比率尺度データ
⇒ Spearman(スピアマン)の順位相関係数
SPSSを使用したスピアマン(Spearman)の順位相関係数-データ入力の方法-
SPSSでスピアマン(Spearman)の順位相関係数を算出する場合にはデータの入力方法は簡単です.
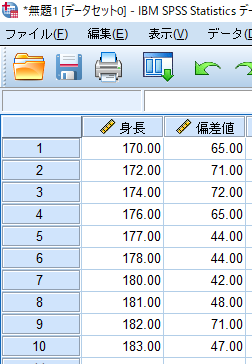
このように横列に関係性を分析したい同一対象者のデータ(身長と偏差値)を並べます.
SPSSを使用したスピアマン(Spearman)の順位相関係数-2変数の関連性を明かにしたい場合-
まずは関連性を明かにしたい変数が2つの場合の方法をご紹介いたします.
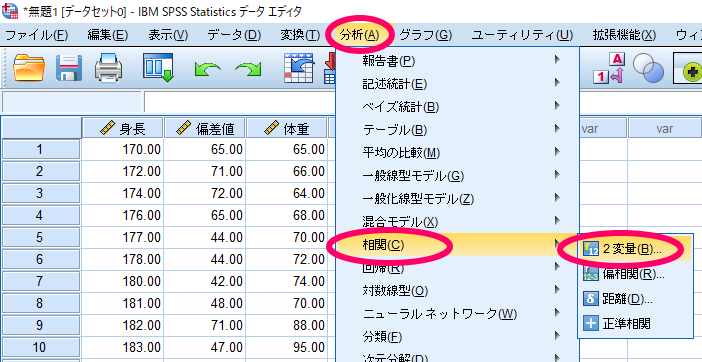
このデータの場合,身長は比率尺度データであり正規分布しておりますが,偏差値は比率尺度データではあるものの非正規分布であったため,ノンパラメトリック検定であるスピアマン(Spearman)の順位相関係数を選択したといったわけです.
SPSSを使用したスピアマン(Spearman)の順位相関係数の結果の見方・確認方法 -2変数の関連性を明かにしたい場合-
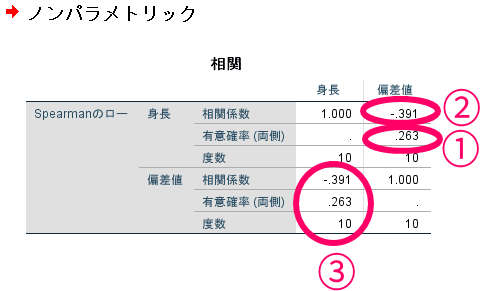
これがスピアマン(Spearman)の順位相関係数の結果です.
相関分析の結果を見る際にははじめに必ず有意確率を確認しましょう.
有意確率(p)<0.05:相関がある
有意確率(p)≧0.05:相関がない(厳密にいえばあるともないとも言えない)
この場合には,有意確率が0.263で5%以上ですので,身長と偏差値には有意な相関はない(厳密にいえばあるともないとも言えない)といった解釈ができます.
有意確率が有意水準未満(ここでは5%)であれば,合わせて相関係数(ρ)を確認します.
ちなみにPearson(ピアソン)の積率相関係数は「r」で表記することが多いですが,Spearmanの順位相関係数は「ρ(ロー)」や「rs」と表記することが多いです.
この場合には有意確率が5%以上ですので相関係数にあまり大きな意味はありません.
仮に有意確率が5%未満であったとして考えると,この場合には相関係数は-0.391であることが確認できます.

相関係数って-0.391って相関が強いの?弱いの?

相関係数には以下のような目安があります.ただこれはあくまで目安であって絶対的な基準ではない点にも注意が必要です.
|ρ|=1.0~0.7
強い相関がある
|ρ|=0.7~0.4
中等度の相関がある
|ρ|=0.4~0.2
弱い相関がある
|ρ|≦0.2
ほとんどなし
今回の場合には相関係数は-0.391ですので身長と体重の間には有意な弱い相関がある(仮に有意確率が5%未満であれば)と解釈できるでしょう.
また相関係数が負の値になっておりますので,負の相関を示していると考えられます.
つまり身長が上がると偏差値が下がるといった関係性があると考えられます.
相関分析を行うと変数の数に応じた表が出力されます.
この場合には変数は身長と体重で2つですので,2×2の表が出力されます.
出力された表には対角線上に同じ有意確率と相関係数が出力されます.
この場合にはどちらの有意確率と相関係数を確認しても問題ありません.
右上は偏差値と身長の関係を,左下は身長と偏差値の関係を見ているわけですが,結局は同じことです.
SPSSを使用したスピアマン(Spearman)の順位相関係数の算出方法-相関行列を作成して3変数以上の関連性を明かにしたい場合-

SPSSを使用したスピアマン(Spearman)の順位相関係数の結果の見方・確認方法 -3変数以上の関連性を明かにしたい場合-
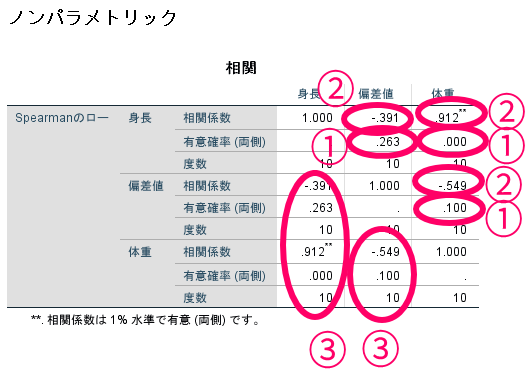
これがSpearman(スピアマン)の順位相関係数の結果です.
相関分析の結果を見る際にははじめに必ず有意確率を確認しましょう.
相関行列の場合には複数の組み合わせの有意確率を確認する必要があります.
有意確率に応じて以下のように解釈します.
有意確率(p)<0.05:相関がある
有意確率(p)≧0.05:相関がない(厳密にいえばあるともないとも言えない)
この場合には,「身長×偏差値」,「身長×体重」,「体重×偏差値」といった3つの組み合わせが考えられますが,有意確率が5%未満なのは「身長×体重」だけですので,身長・体重の間には有意な相関がある,身長・偏差値間および体重・偏差値間には有意な相関が無い(厳密にいえばあるともないとも言えないといった解釈ができます.
ちなみに関係性を分析したい変数の数が増えると表から有意な相関が得られた数値を読み取るのに時間がかかります.
そのためSPSSでは有意確率が5%または1%未満のものにはアスタリスク(*)が表記されるようになっております.
ちなみに有意確率が1%未満であればアスタリスクが2つ,有意確率が5%未満であればアスタリスクが1つ表示されます.
有意確率が有意水準未満(ここでは5%)であれば,合わせて相関係数(ρ)を確認します.
この場合には有意確率が5%未満のものは「身長×体重」だけですので,「身長×体重」の相関係数をみると相関係数(ρ)は0.912であることがわかります.
その他の「身長×偏差値」,「体重×偏差値」の相関係数については,有意確率が5%以上ですので相関係数の値自体は大きな意味を持ちません.
|ρ|=1.0~0.7
強い相関がある
|ρ|=0.7~0.4
中等度の相関がある
|ρ|=0.4~0.2
弱い相関がある
|ρ|≦0.2
ほとんどなし
今回も「身長×体重」の相関係数(ρ)が0.7を上回っておりますので,身長・体重の間には強い相関があると解釈できるでしょう.
相関分析を行うと変数の数に応じた表が出力されます.
この場合には変数は身長・体重・腹囲で3つですので,3×3の表が出力されます.
出力された表には対角線上に同じ有意確率と相関係数が出力されているのが確認できます.
この場合にはどちらの有意確率と相関係数を確認しても問題ありません.
SPSSを用いてスピアマン(Spearman)の順位相関係数を行った際のグラフ作成
Spearman(スピアマン)の順位相関係数を用いる場合には2変数の関連性を分析することとなりますので,Spearman(スピアマン)の順位相関係数を用いた場合に使用すべきグラフは散布図です.
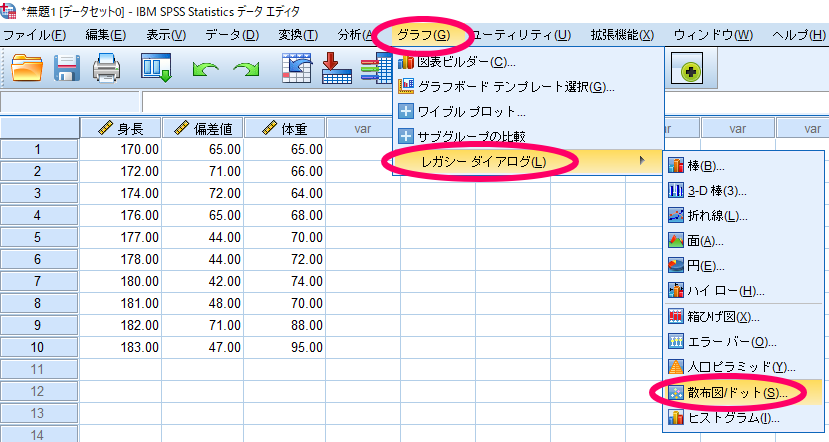
オプションは特に設定する必要はありません.
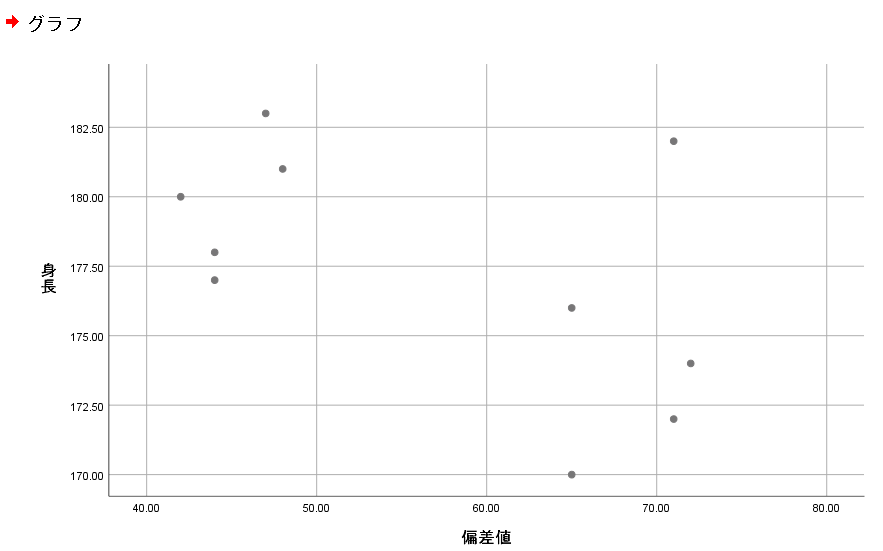
これが完成した散布図です.
この散布図からも身長と偏差値の間にはこれといった関係性は無さそうですね.
Spearman(スピアマン)の順位相関係数における効果量(r)の算出

相関分析でも効果量の算出が必要なの?

いえ,必要ありません.実は相関分析では有意確率と合わせて相関係数をみるのが一般的です.実はこの相関係数というのが効果量に当たるものですので,相関分析の場合には効果量を改めて算出する必要はありません.



コメント
[…] 2変数の関係性を見る方法については,パラメトリックの検定であるPearson(ピアソン)の積率相関係数とノンパラメトリックの検定であるSpearman(スピアマン)の順位相関係数についてご紹介させていただきました. […]