相関分析の際の注意点
2変数の関係性を見る方法については,パラメトリックの検定であるPearson(ピアソン)の積率相関係数とノンパラメトリックの検定であるSpearman(スピアマン)の順位相関係数についてご紹介させていただきました.
相関分析は頻繁に行われる手法ですが,結果の解釈も慎重に行う必要があります.
今回は相関分析を行う際の注意点についてご紹介させていただきます.

相関分析を行う時にどういった点に注意したらいいの?

まず相関分析の結果を解釈する際には,有意確率を過信しないといった点が重要です.また疑似相関にも注意が必要です.交絡を考慮した上で偏相関分析を用いるなどの対応が必要です.さらに時系列データへは相関分析は適応できないといった点にも注意が必要です.加えて学会発表では相関関係=因果関係と解釈して発表している方がおられますが基本的には誤りです.後に詳細に解説をしますね.
有意確率を過信しない
①相関分析で有意確率が5%未満か否かを確認する
疑似相関に注意
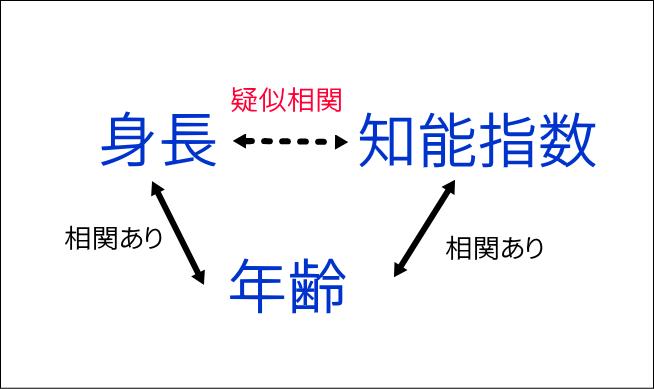
例えば小学生の身長と知能指数と年齢との関係について考えてみたいと思います.
まず小学生の身長と年齢に相関関係があることには異論はないと思います.
また小学生の知能指数と年齢にも相関があることには異論はないと思います.
では知能指数と身長ってどうでしょうか?
背が高いほど知能指数が高いと言われてもなんかしっくりこないと思います.
実は身長と知能指数は年齢といった交絡が介在することで疑似相関を呈しているのです.
つまり身長と知能指数に本当に関連があるかどうかは,身長と知能指数の相関関係を調べるだけではよくわからないということになります.
そのため身長と知能指数の間に本当に関連性があるかどうかを調べるためには,年齢を考慮した上で身長と知能指数との関連性を調べる必要があります.
こういった場合に偏相関分析を用いることで,年齢を考慮した上で身長と知能指数の間に関連性があるのかどうかを明らかにすることができるといった点については過去にも偏相関分析の記事でご紹介いたしました.
時系列データへの相関分析の適応
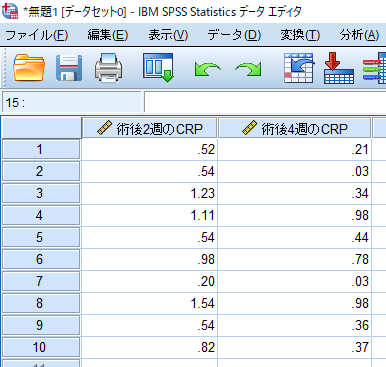
例えば術後2週と術後4週のCRPのデータがあったとします.
このデータを使って術後2週から術後4週にかけて炎症反応が鎮静化するといったような経時的な変化を明らかにすることはできません.
このような場合には回帰分析か分散分析を適応すべきです.
相関係数を算出する場合には互いに無作為抽出され多標本であることが前提になりますので,同一対象を経時的に観察したデータに相関分析を適応することはできません.
相関関係=因果関係ではない
相関分析というのはあくまで2変数の関連性の高さを分析しているにすぎませんので,2変数のうちどちらが原因でどちらが結果でといった因果関係の部分にまで踏み込むことはできません.
1)犯罪者の98%はごはんを食べている
2)ごはんを食べて育った子供の約半数は, テストが平均点以下
3)暴力的犯罪の90%は, ごはんを食べて24時間以内に起きている
4)出生後2週間の新生児にごはんを与えると, 全例がのどをつまらせて苦しがる
5)1800年代, ごはんを主食としていた日本人の平均寿命は40歳代であった
これをみてどう思われますか?
ご飯って危険な食べ物だなって思いますか?
この例を見ればわかるように相関関係=因果関係ではないというのは明白です.

なぜ相関関係=因果関係ではないの?

相関関係=因果関係では大きく分類すると以下の3つの分類することができます!

相関がどうこうも大切ですが,専門的見地からどういった機序で因果の存在を説明できるかを考えることが最も重要ですね!





コメント