SPSSによる重回帰分析の概要
多変量解析の中で最も使用頻度が高いのが重回帰分析です.
まずは重回帰分析がどのような解析かを簡単に整理したいと思います.
例えば対象者の年齢をもとに年収を予測したい場合には,従属変数yを年収,独立変数xを年齢として
年収(y)=a+b×年齢(x)
と考えます.
ただ年収に影響を与える要因というのは年齢だけではないですよね?
例えば学歴とか残業時間とか他にも要因が考えられます.
そのため
年収(y)=a+b1×年齢(x1)+b2×学歴(x2)+b3×残業時間(x3)
と複数の要因を含めて年収を予測した方がより高い精度で年収を予測することができます.
このような独立変数xが2つ以上ある式を重回帰式とよび,重回帰分析を用いて作成されます.
SPSSによる重回帰分析の適用条件
・従属変数yに対して独立変数xの影響度合いを解析したり,従属変数yの予測式を構築するために用いる
・従属変数yは量的変数で1つ
・独立変数xは量的変数(ダミー変数化も可能)で2つ以上
・基本的に従属変数・独立変数ともすべて正規分布に従うことが望ましい(実際には予測式から算出される予測値と実測値の誤差(残差)が正規分布に従えば問題ない.詳細は口述)
SPSSによる重回帰分析の目的
SPSSによる重回帰分析の目的は①予測式を求める,②従属変数に対する独立変数の影響の程度を検討するといった2つに分類できます.
予測式を求める
予測式として用いる場合には後述する決定係数が高いことが重要となります.
決定係数が低いと予測式としての価値が低くなります.
年収(y)=a+b1×年齢(x1)+b2×学歴(x2)+b3×残業時間(x3)
この場合には年齢・学歴・残業時間から年収を予測することになりますが,予測の的中度が低ければあまり意味がありませんよね.
従属変数に対する独立変数の影響の程度を検討する
一方で従属変数に対する独立変数の影響の程度を検討する場合には,あまり高い決定係数は求められず,むしろ口述する各独立変数の有意性や決定係数の値,係数の信頼区間が重要となります.
年収(y)=a+b1×年齢(x1)+b2×学歴(x2)+b3×残業時間(x3)
この場合には最終的に年齢・学歴・残業時間の中でもどの要因が年収との関連が大きくなるのかといった視点が重要となりますので,決定係数自体は低くとも問題ありません.
SPSSによる重回帰分析の手順
SPSSによる重回帰分析は以下の手順で行います.
①従属変数yと独立変数xの決定
②事前準備
- 名義尺度データのダミー変数化
- 多重共線性の考慮
- 標本の大きさと独立変数の数の考慮
③独立変数の投入
- ステップワイズ法を優先
④重回帰式の有意性を判定
- 分散分析表の判定
- 偏回帰係数が全て有意水準未満
⑤重回帰式の適合度を評価
- 重相関係数R,決定係数R2を優先
⑥残差分析
- 外れ値のチェック
- ランダム性,正規性の確認
①従属変数yと独立変数xの決定
まずは従属変数と独立変数を決定します
年収(y)=a+b1×年齢(x1)+b2×学歴(x2)+b3×残業時間(x3)
この例でいえば年収が従属変数,年齢・学歴・残業時間が独立変数ということになります.
②事前準備
名義尺度データのダミー変数化
重回帰分析では従属変数,独立変数ともに量的変数を用いる必要があります.
そのため名義尺度のデータは量的変数として扱えるようにダミー変数化する必要があります.
年収(y)=a+b1×年齢(x1)+b2×学歴(x2)+b3×残業時間(x3)

この例でいえば学歴(専門学校卒業・大学卒業)が名義尺度変数になりますので,これを量的変数に変換する必要があります.
名義尺度変数以外でも順序尺度変数や正規分布に従わない間隔・比率尺度変数をダミー変数化する場合もあります.
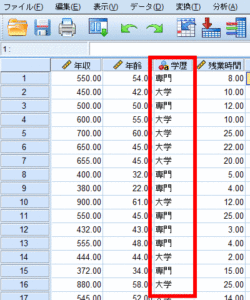
ここでは学歴をダミー変数化する方法について解説します.
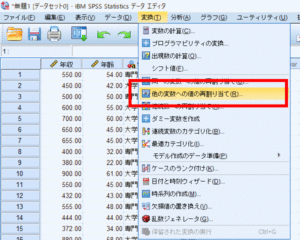
まず変換から他の変数への値の再割り当てを選択します.
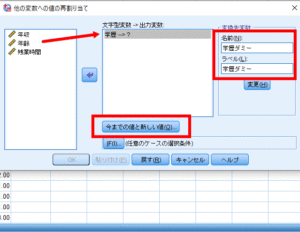
学歴を文字型変数→出力変数に移動させ,変換先変数の名前・ラベルを「学歴ダミー」と入力した上で「変更」をクリックして,「今までの値と新しい値」をクリックします.
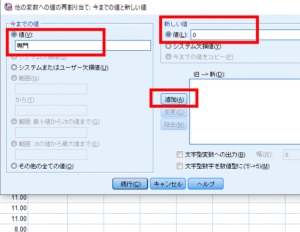
今までの値に「専門」,新しい値に「0」と入力して追加をクリックします.
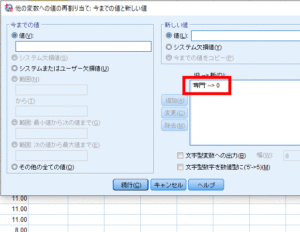
そうすると「旧→新」の欄に「専門→1」と追加されます.
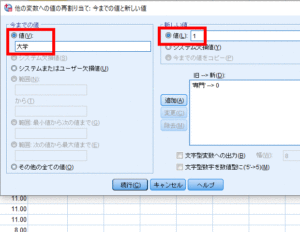
同様に「大学」を「1」に変換します.
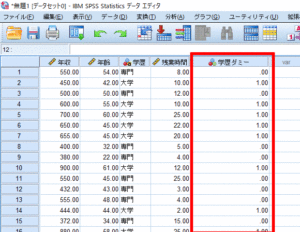
これでダミー変数化が完了しました.
多重共線性の考慮

多重共線性って何なの?

多重共線性というのは独立変数間の関連性が高すぎる場合に起こる様々な問題を指します.一般的には独立変数間に相関係数が1に近い関連性がある場合や,独立変数の個数が標本(データ数)の大きさに比べて大きい時に生じることがあります

多重共線性があるかをどうやって判断したらいいの?

多重共線性の有無を判断するには3つの方法があります
①独立変数間の相関行列から相関係数が1に近い変数が無いかを観察する
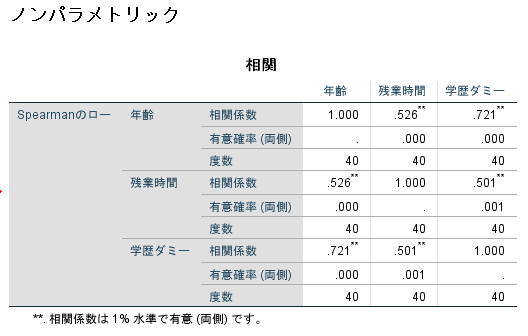
ここでは3つの独立変数間の相関に関してSpearmanの順位相関係数を用いて検討しましたが,rが0.80をこえる関連性は見られませんでした.
多重共線性を判断する場合にどの程度相関係数が高いと問題なのかについては明確な基準は存在しませんが,r>0.80が1つの基準になるでしょう.
ちなみに独立変数間にr>0.80となる高い関連性を有する独立変数が存在する場合には,どちらか一方の独立変数を削除するのが一般的です(専門的見地から考慮した上で削除することが重要です).
②R2がきわめて高いにもかかわらず標準偏回帰係数または偏相関係数が極端に小さい独立変数がある
③分散インフレ係数(variance inflation factor;VIF)が10以上
この②と③の方法については重回帰分析を行った後に,出力された結果から多重共線性の有無を判断することになります.
標本の大きさと独立変数の数の考慮 必要なサンプルサイズは?
重回帰分析をはじめとする多変量解析では独立変数の数に対する標本の大きさ(サンプルサイズ=データの数)が重要となります.
サンプルサイズに対して独立変数の数が大きいと重回帰式の精度が悪くなってしまいます.
どのくらいのサンプルサイズが必要かについては明確な基準は存在しませんが一般的には以下のような基準を参照すると良いでしょう.
サンプルサイズ≧2×独立変数の数(Trapp, 1994)
サンプルサイズ≧3~4×独立変数の数(本多, 1993)
サンプルサイズ≧10×独立変数の数(Altman, 1999)
サンプルサイズ≧200(Kline, 1994)
この場合の独立変数の数というのは投入する独立変数の数ではなく,最終的に抽出された独立変数の数であるといった点にも注意が必要です.
③独立変数の投入方法
重回帰分析では複数の独立変数を投入するわけですが,独立変数の投入方法によっても結果が大きく変化します.
独立変数の投入方法については大きく分類すると①強制投入法と②ステップワイズ法の2つの方法が用いられます.
①強制投入法
研究者の専門的見地から主観で独立変数を決定して投入する方法になります.
先ほどの例では年収に対して,年齢・学歴・残業時間が影響するはずだと考えて,重回帰分析を行います.
②ステップワイズ法
有意水準や統計量の変化を理論的に観察しながら,独立変数を取り込んだり除外したりして,少しずつ適した重回帰式に近づける方法です.
強制投入法よりも推奨される方法ですが,変数増加法・変数減少法・変数増減法などがあります.
③強制投入法+ステップワイズ法
場合によっては強制投入法とステップワイズ法を組み合わせて行う方法もあります.
交絡として必ず投入したい変数を強制投入で投入して,その他の要因をステップワイズ法で投入するといった方法です.
この場合には階層的に重回帰分析を実施することとなります.
ステップワイズ法をはじめとする変数自動選択の手法はとても便利ですが,全自動で常に理想的な重回帰式が構築されるとは限りません.
専門的見地からこの変数は必ず残すべきとか,この変数は必要ないと考えることもあると思います.
機械的な自動選択では独立変数間の構造を無視した重回帰式が構築され,解釈が困難になる場合もあります.
SPSSを用いた重回帰分析の実際
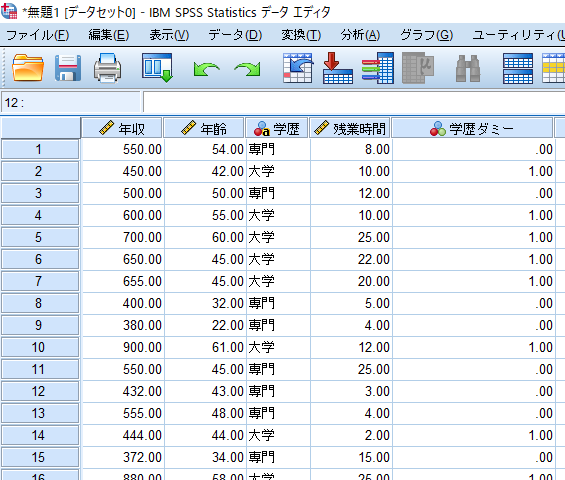
データを用意します.
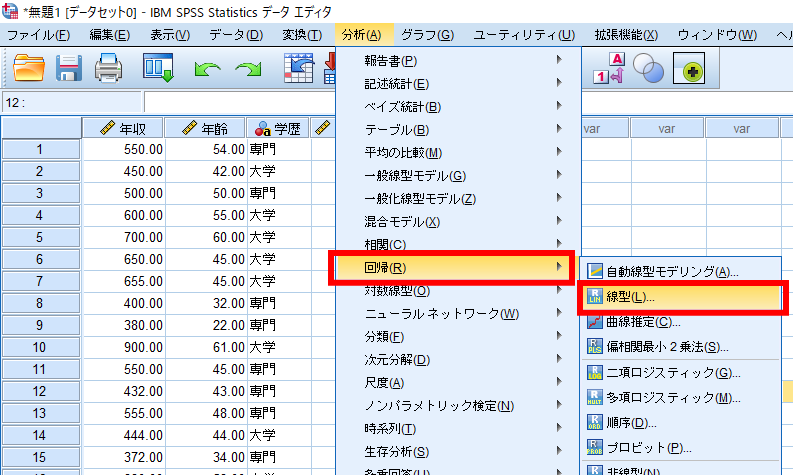
「分析」→「回帰」→「線型」の順で選択します.
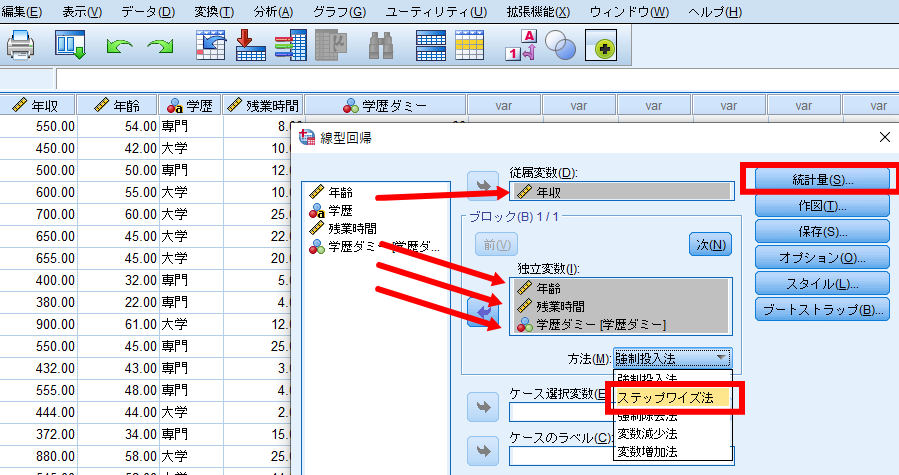
年収を従属変数へ移動させます.
年齢・学歴(ダミー変数にしたもの)・残業時間を独立変数へ移動させます.
変数投入法はステップワイズ法を選択します.
統計量をクリックします.
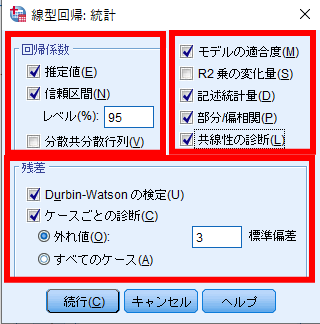
回帰係数の「推定値」・「信頼区間」にチェックします.
また「モデルの適合度」・「記述統計量」・「部分/偏相関」・「共線性の診断」にチェックを入れます.
残差の「Durbin-Watsonの検定」と「ケースごとの診断」にチェックを入れ,外れ値が3標準偏差となっていることを確認します.
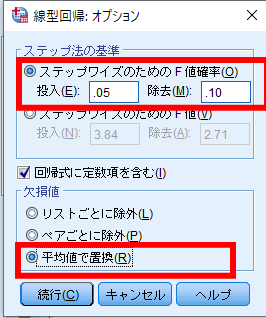
オプションを選択しステップ法の基準のステップワイズのためのF値確立にチェックが入り,投入が0.05,除去が0.10となっていることを確認します.
また欠損値の処理は平均値で置換にチェックを入れます.
続きは後編でご確認ください.
SPSSによる重回帰分析 結果の見方は?結果の書き方は?結果の解釈の方法は?残差分析は?ダービン・ワトソン比(Durbin-Watson ratio)って?(後編)






コメント
[…] SPSSによる重回帰分析 多重共線性って?ダミー変数って?必要なサンプル… […]
[…] SPSSによる重回帰分析 多重共線性って?ダミー変数って?必要なサンプル… […]