SPSSによる重回帰分析の手順
SPSSによる重回帰分析(前編)でもご説明させていただきましたが,SPSSによる重回帰分析は以下の手順で行います.

①従属変数yと独立変数xの決定
②事前準備
- 名義尺度データのダミー変数化
- 多重共線性の考慮
- 標本の大きさと独立変数の数の考慮
③独立変数の投入
- ステップワイズ法を優先
④重回帰式の有意性を判定
- 分散分析表の判定
- 偏回帰係数が全て有意水準未満
- 多重共線性の判断
⑤重回帰式の適合度を評価
- 重相関係数R,決定係数R2を優先
⑥残差分析
- 外れ値のチェック
- ランダム性,正規性の確認
③の独立変数の投入までは前編で方法をご紹介させていただきましたので,今回は主に重回帰分析結果の見方について説明させていただきます.
④重回帰式の有意性を判定
重回帰モデルの有意性の判断
SPSSで重回帰分析を行うとさまざまな結果が出力されますが,まず分散分析表を確認します.
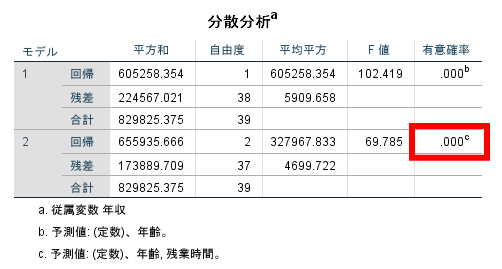
分散分析表にはモデルが複数出力されることもありますが,基本的に最も下位のモデルを参照すれば問題ありません.
なぜモデルが複数出力されるかですが,重回帰分析では変数を1つずつ増やしたり減らしたりしていった経過を表しております.
最終的に選ばれた最適モデルの組合せが一番下のモデルというわけです.
次に分散分析表の有意確率(赤線で囲んだ部分)を参照します.
この有意確率が5%未満であれば有意に役に立つ重回帰式であるといえるでしょう.
逆に有意確率が5%以上であればこの重回帰式は役に立ちません.
今回は有意確率が0.000となっておりますので重回帰式として意味を成すと解釈できます.
独立変数の有意性の判断
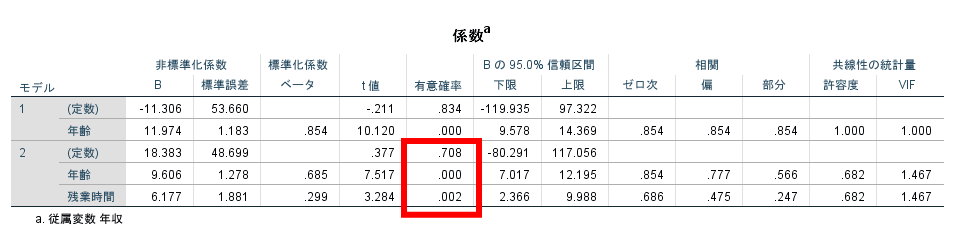
次に係数と書かれている表を参照します.
この係数の有意確率(赤枠の部分)を参照します.
この有意確率が5%未満であればその変数を重回帰式に組み込むことになります.
仮に5%以上の変数があればその変数を除いて解析を行うか,その変数は従属変数との関連が低いと考えることができるでしょう.
この場合には年齢と残業時間は有意確率が5%未満ですので,年齢や残業時間は年収との関連性が高いと考えられます.
ステップワイズ法の場合には有意確率が5%未満の変数しか抽出されませんが,強制投入の場合には有意確率が5%以上の変数もモデルに含まれます.
独立変数の影響度合の判断
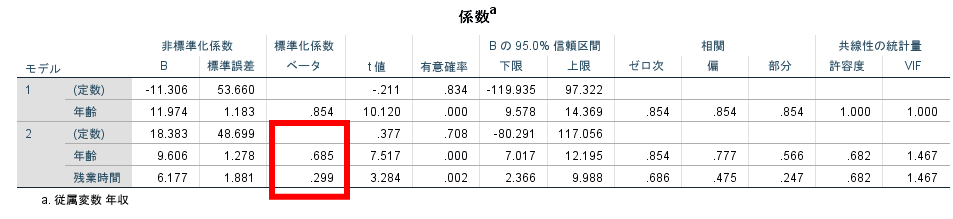
各独立変数がどの程度従属変数と関連しているのかについては標準化係数を参照するとよいです.
この標準化係数は独立変数の単位に依存しない係数ですので,単純に係数の大きさを比較することで従属変数に関する影響力を比較することができます.
この場合であれば年収に最も大きな影響を及ぼすのは年齢であり,次に残業時間であると考えることができます.
重回帰式の作成
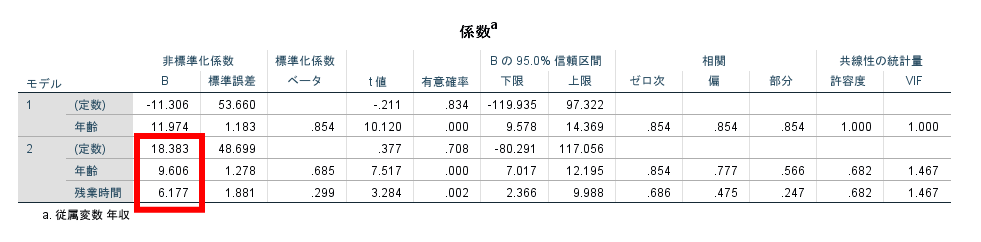
従属変数に対する独立変数の影響度合を見るためには,標準化係数を参照することになりますが,重回帰式を作成する場合には非標準化係数を参照します.
この場合には以下のような重回帰式が完成します.
年収=年齢×9.606+残業時間×6.177+18.383(定数)
となります.
多重共線性の判断
多重共線性については前編でご紹介させていただきました.
再度復習ということで…

多重共線性って何なの?

多重共線性というのは独立変数間の関連性が高すぎる場合に起こる様々な問題を指します.一般的には独立変数間に相関係数が1に近い関連性がある場合や,独立変数の個数が標本(データ数)の大きさに比べて大きい時に生じることがあります

多重共線性があるかをどうやって判断したらいいの?

多重共線性の有無を判断するには3つの方法があります
①独立変数間の相関行列から相関係数が1に近い変数が無いかを観察する
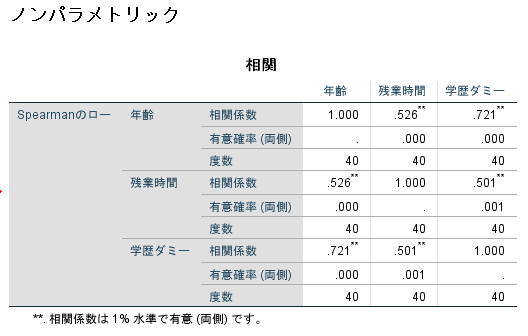
ここでは3つの独立変数間の相関に関してSpearmanの順位相関係数を用いて検討しましたが,rが0.80をこえる関連性は見られませんでした.
多重共線性を判断する場合にどの程度相関係数が高いと問題なのかについては明確な基準は存在しませんが,r>0.80が1つの基準になるでしょう.
ちなみに独立変数間にr>0.80となる高い関連性を有する独立変数が存在する場合には,どちらか一方の独立変数を削除するのが一般的です(専門的見地から考慮した上で削除することが重要です).
②R2がきわめて高いにもかかわらず標準偏回帰係数または偏相関係数が極端に小さい独立変数がある
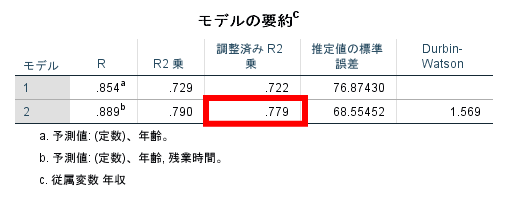
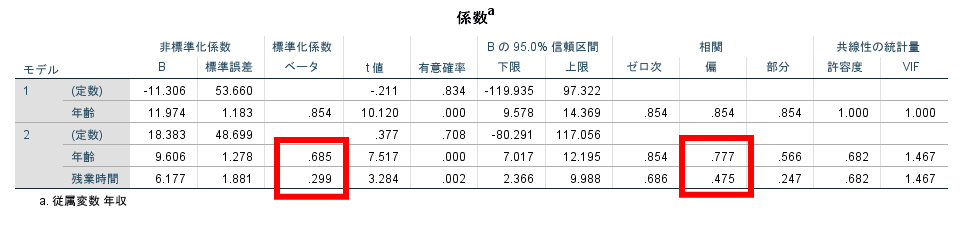
この場合には調整済みR2は高いものの,標準化係数や偏相関係数も極端に小さくありませんので,多重共線性が生じている可能性は低いと考えられます.
③分散インフレ係数(variance inflation factor;VIF)が10以上
多重共線性を客観的に判断するにはこのVIFを用いた判断が最も勧められます.
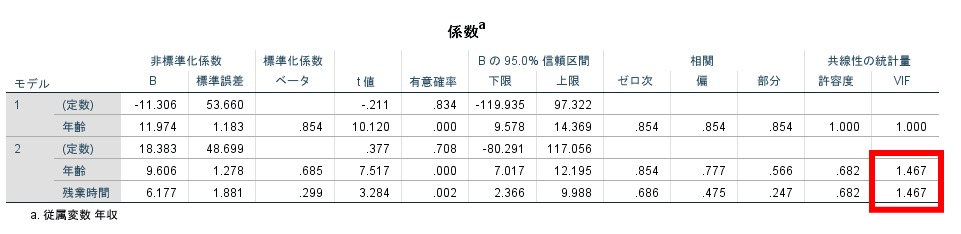
この場合にはVIFが2変数ともに10以下(VIF<10)ですので,多重共線性が生じた可能性は低いと考えられます.
⑤重回帰式の適合度の評価

重回帰式の適合度とは重回帰式の当てはまりの良さを意味します.
重相関係数Rは重回帰式の当てはまりの良さを表す指標ですが,一般的にはR>0.7が理想とされます.
重相関係数Rがそのまま用いられることは少なく決定係数R2として用いられることが多いです.
決定係数R2は重相関係数を2乗した値ですが,一般的にはR2>0.5が理想とされます.
R2は従属変数のバラツキを重回帰式の中の独立変数で何%説明できるかを意味します.
また独立変数の数によっても重相関係数は変化しますので,この独立変数の数を調整した自由度調整済決定係数(調整済R2)を用いるのが一般的です.
ここでは調整済R2は0.779でありますので重回帰式の適合度はかなり高いと考えてよいでしょう.
この場合には年収のバラツキの77.9%は年齢と残業時間で説明できると考えることができるでしょう.
⑥残差分析
最後に残差分析です.
重回帰分析では基本的に従属変数・独立変数ともすべて正規分布に従うことが望ましいわけですが,実際には予測式から算出される予測値と実測値の誤差(残差)が正規分布に従えば問題ありません.
データの残差は確立の法則に従ってランダムな値を取ることが知られておりますが,残差が規則的に変動する場合にはデータに何らかの問題がある可能性があります.
残差の正規性を確認する上ではまずはダービン・ワトソン比(Durbin-Watson ratio)を参照することが重要です.
ダービン・ワトソン比(Durbin-Watson ratio)は残差がランダムであれば2に近づくことが知られており,残差がランダムでなく正の相関があれば0に近づき,負の相関があれば4に近づきます.
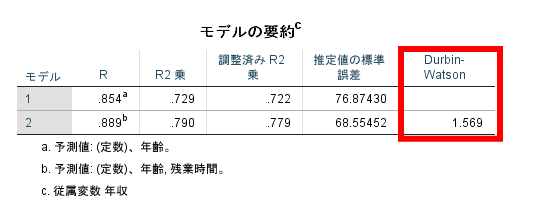
この場合にはダービン・ワトソン比(Durbin-Watson ratio)は1.569と比較的2に近いので,残差はランダムである可能性が高いと考えられます.
ダービン・ワトソン比(Durbin-Watson ratio)だけでは心配な場合には残差の正規性を確認する方法もあります.
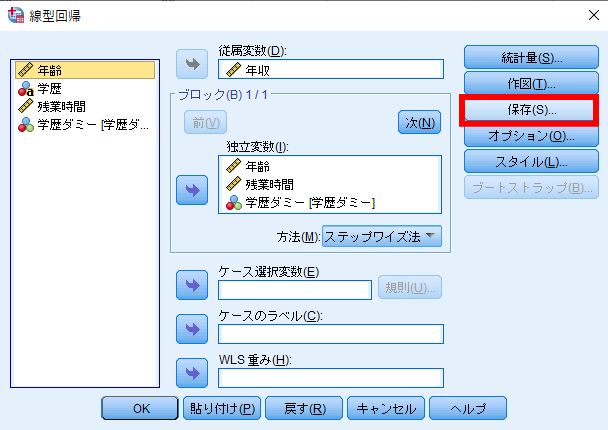
線形回帰の保存ボタンを押すと以下のような表示がなされます.
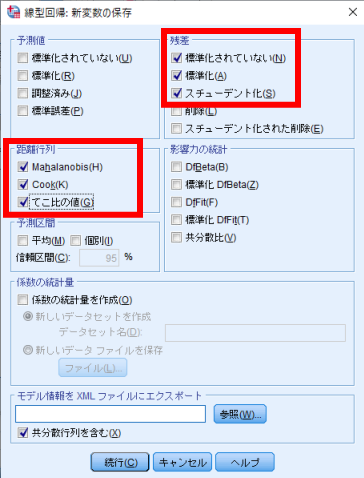
残差の上3つの部分に,距離行列の3つにチェックを入れて重回帰分析を行います.
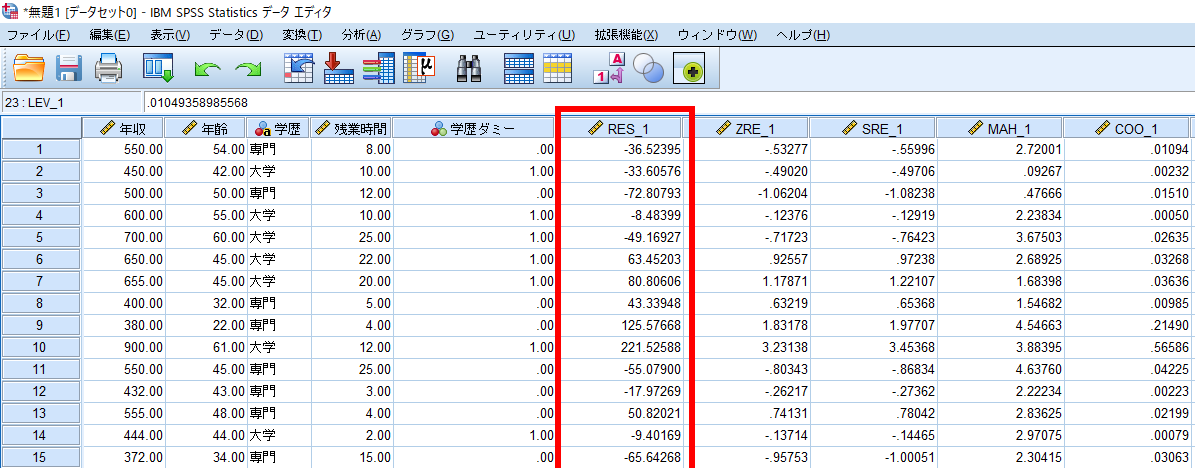
そうするとデータセットにRES_1といったデータが出力されます.
このRES_1が残差(予測値と実測値の誤差)になります.
Shapiro-Wilk検定を用いて残差の正規性を確認します.
SPSSによる正規性の検定Shapiro-wilk(シャピロウィルク)検定
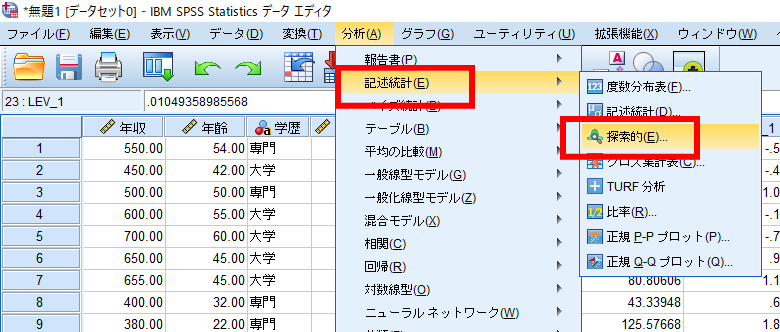
「分析」→「記述統計」→「探索的」と選択します.
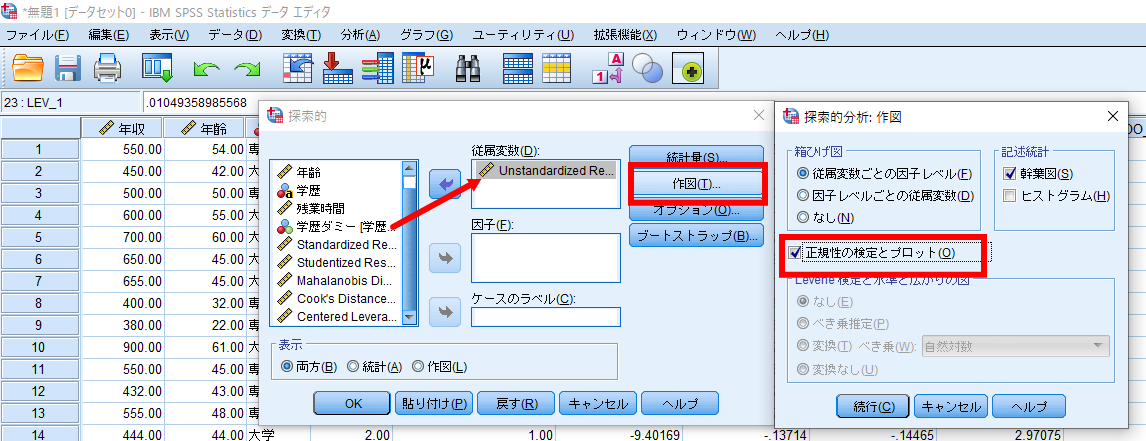
Unstandardized Residual(RES_1)を従属変数へ移動させて作図をクリックします.
正規性の検定とプロットをチェックすれば完了です.
Shapiro-Wilk検定の結果がp≧0.05であれば残差の正規性が確認できたということになります.
論文・学会発表での重回帰分析の結果の書き方
- 学会発表や論文には以下の点を記載します.
- 変数のダミー変数化,変数変換を行った場合にはそれに至った理由
- 多重共線性の確認を行ったか
- 変数選択にはどの方法を使ったか
- 的高度の評価は何を指標としたか
- 残差,外れ値の検討をしたか
論文への記載例
事前に変数の正規性についてShapiro-Wilk検定を用いて分析を行ったところ量的変数については正規性が確認された.
名義尺度変数である学歴についてはダミー変数化した.
また相関行列表を観察した結果,|r|>0.8となるような変数は存在しなかったため全ての変数を対象とした.
VIFは全て10.0未満であり多重共線性には問題が無かった.
ステップワイズ法(変数増減法)による重回帰分析の結果は以下の通りであった.
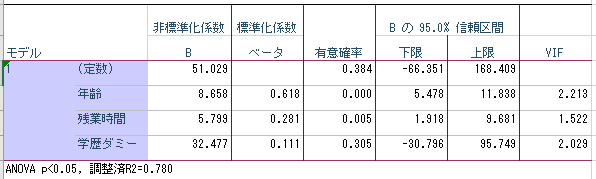
ANOVA(分散分析表)の結果は有意で,調整済R2は0.78であったため,適合度は高いと評価した.
ダービン・ワトソン比は1.569であり,実測値に対して予測値が±3SDを超えるような外れ値も存在しなかった.





コメント
[…] SPSSによる重回帰分析 結果の見方は?結果の書き方は?結果の解釈の方法… […]
[…] SPSSによる重回帰分析 結果の見方は?結果の書き方は?結果の解釈の方法… […]