階層的重回帰分析とは?
階層的重回帰分析というのはステップ1からステップ2へとステップごとに変数を投入していく主要です.
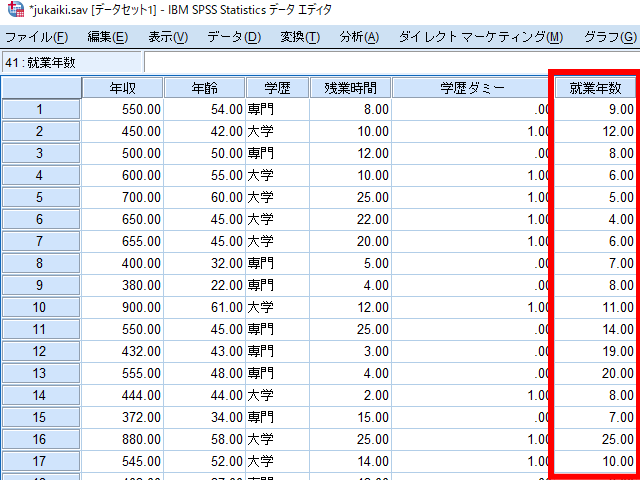
ここでは年齢,学歴,残業時間,就業年数が年収に与える影響について重回帰分析を用いて検討する例をみて階層的重回帰分析について解説をいたします.
階層的重回帰分析の意義を理解する上では,まず独立変数の投入方法について理解することが重要です.
独立変数の投入方法
重回帰分析では複数の独立変数を投入するわけですが,独立変数の投入方法によっても結果が大きく変化します.
独立変数の投入方法については大きく分類すると①強制投入法と②ステップワイズ法の2つの方法が用いられます.
①強制投入法
研究者の専門的見地から主観で独立変数を決定して投入する方法になります.
先ほどの例では年収に対して,年齢・学歴・残業時間・就業年数が影響するはずだと考えて,重回帰分析を行います.
②ステップワイズ法
有意水準や統計量の変化を理論的に観察しながら,独立変数を取り込んだり除外したりして,少しずつ適した重回帰式に近づける方法です.
強制投入法よりも推奨される方法ですが,変数増加法・変数減少法・変数増減法などがあります.
③強制投入法+ステップワイズ法
場合によっては強制投入法とステップワイズ法を組み合わせて行う方法もあります.
交絡として必ず投入したい変数を強制投入で投入して,その他の要因をステップワイズ法で投入するといった方法です.
例えば就業年数は年収に影響を与えるのは当然なので,就業年数を考慮した上で年齢,学歴,残業時間が年収と関連するかどうかを検討したいとします.
このような場合に用いられるのがこの場合には階層的重回帰分析です.
階層的重回帰分析ではいくつかのステップに分けて独立変数を投入します.
ステップ1:就業年数(強制投入法)
ステップ2:年齢・学歴・残業時間(ステップワイズ法)
このように2つのステップをふむことで,就業年数を考慮した上で年齢・学歴・残業時間のどういった要因が年収と関連するかを明らかにすることが可能となります.
階層的重回帰分析と重回帰分析の手順の相違
具体的な階層的重回帰分析の手順は重回帰分析と同様ですので,以下のリンクをご参照ください.

階層的重回帰分析の手順で一般的な重回帰分析と大きく異なるのは独立変数の投入方法です.
ここでは独立変数の投入方法についてステップをふんで実施する流れについて解説させていただきます.
階層的重回帰分析の手順
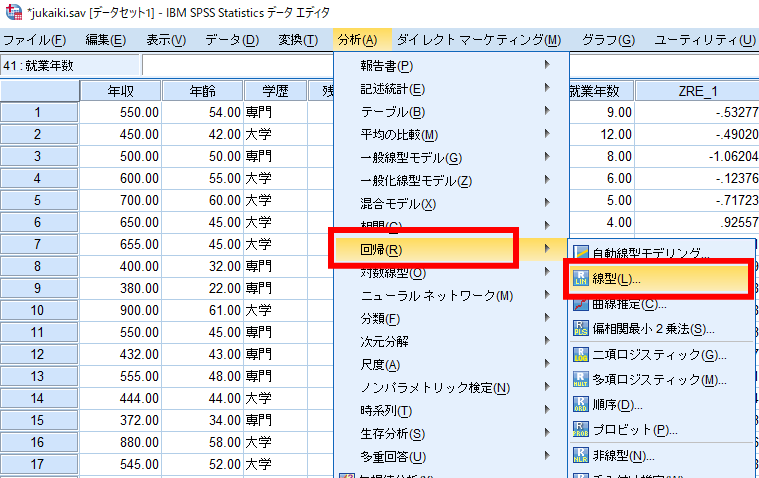
まず「分析」→「回帰」→「線形」と選択します.
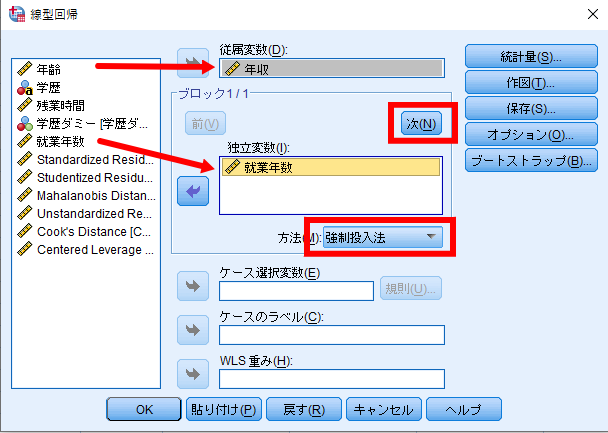
はじめに年収を従属変数へ移動させます.
独立変数の中から交絡として投入したい就業年数を独立変数へ移動させ,強制投入法を選択した状態で,「次」のボタンをクリックします.
この操作がステップ1となります.
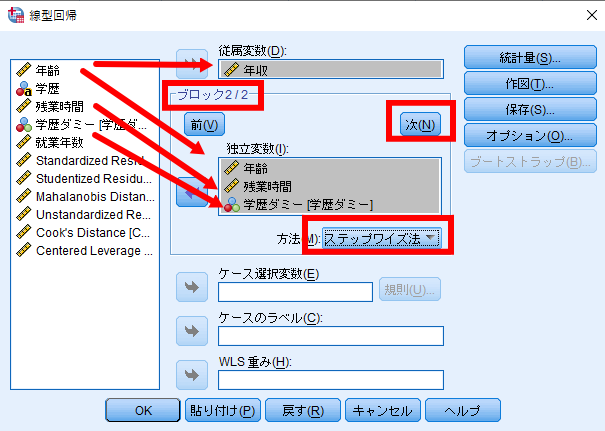
ここからがステップ2です.
まずブロック2/2(赤枠の部分)と表記されていることを確認します.
その上で年齢,残業時間,学歴ダミーを独立変数に移動させます.
変数投入方法はステップワイズ法を選択します.
ここからは通常の重回帰分析と同様です.
統計量をクリックします.
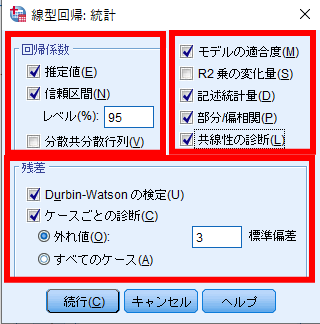
回帰係数の「推定値」・「信頼区間」にチェックします.
また「モデルの適合度」・「記述統計量」・「部分/偏相関」・「共線性の診断」にチェックを入れます.
残差の「Durbin-Watsonの検定」と「ケースごとの診断」にチェックを入れ,外れ値が3標準偏差となっていることを確認します.
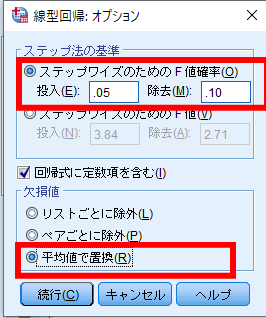
オプションを選択しステップ法の基準のステップワイズのためのF値確立にチェックが入り,投入が0.05,除去が0.10となっていることを確認します.
また欠損値の処理は平均値で置換にチェックを入れます.
階層的重回帰分析の結果の見方
基本的は重回帰分析の結果の見方については以下をご参照ください.

ここでは階層的重回帰分析の結果の見方について通常の重回帰分析とは異なる独立変数の有意性の判断と独立変数の影響度合いの見方について解説いたします.
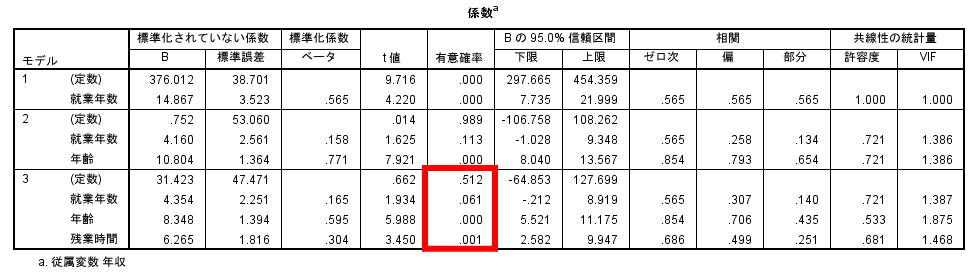
まず係数の有意確率(赤枠の部分)の見方ですが,これは基本的には通常の重回帰分析と同様です.
この有意確率が5%未満であればその変数を重回帰式に組み込むことになります.
階層的重回帰分析の場合には,交絡として就業年数を強制投入しておりますので,最終モデルに係数が有意でない変数(この場合,就業年数 p=0.061)も含まれるといった点です.
このモデルでは就業年数は有意確率が5%以上ですので就業年数は年収と有意な関連性は無いと考えられます.
一方で年齢や残業時間は就業年数を考慮しても年収と関連があると解釈できます.
就業年数が長くなれば年収が上がるのは当たり前ですが,就業年数を考慮しても年齢や残業時間と年収との関連が大きいといった結果が得られます.
このように階層的重回帰分析を使用してステップを踏みながら変数を投入することで,交絡を調整した上で独立変数と従属変数との関連性を明らかにすることが可能となります.





コメント