SPPSによる多重ロジスティック回帰分析の結果の見方をわかりやすく解説 ロジスティック回帰モデルにおけるオッズ比とは? 偏回帰係数・AIC・Hosmer-Lemeshow(ホスマーレミショー)検定って何?
前回の記事で多重ロジスティック回帰分析の方法についてご紹介させていただきました.
ここでは多重ロジスティック回帰分析の結果の見方についてご紹介させていただきます.

多重ロジスティック回帰分析の有意性を判定する指標
SPSSではロジスティック回帰式の要約として回帰式の有意性を判定する指標が出力されます.
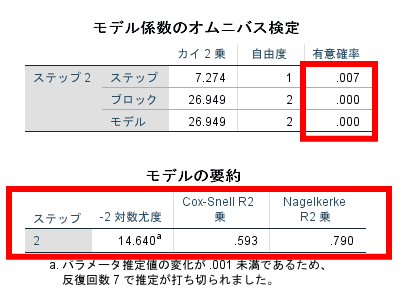
基本的には上のモデルχ2値Model Chi-squareを参照して回帰式の有意性を判断します.
この場合にはモデルの有意確率が5%未満ですので回帰式の有意性が確認できたと解釈して問題ありません.
ちなみにモデルの要約として-2対数尤度やCox-Snell R2やNagelkerkeのR2も出力されますが,基本的にはモデルχ2の有意確率を参照すれば問題ありませんので,この数値は無視しても問題ありません.
-2×対数尤度は絶対基準ではなく相対基準です.
回帰式が完全に適合する場合には尤度は1,-2×対数尤度は0となります.
Cox-Snell R2やNagelkerkeのR2に関しては明確な基準はありませんが高いほど良いと考えておけばよいでしょう.
オッズ比

オッズ比って何?

オッズ比というのは独立変数の影響の大きさを表す指標です.
例えばロジスティック回帰分析を行って従属変数と関連する独立変数が複数抽出された場合には,各独立変数のオッズ比を確認すればどの独立変数の影響力が大きいのかを確認することができます.

調整オッズ比なんて言葉も聞きますが何が違うのですか?

独立変数が複数存在する多重ロジスティック回帰分析では調整オッズ比というのが正確です.調整オッズ比というのは他の独立変数の影響を除外した影響の大きさと考えると良いでしょう.

オッズ比というのは独立変数が1変化した時のオッズ比を出力しています.例えば年齢のオッズ比が2.0であれば今回の例で言うと1歳年を重ねると2倍虫歯になりやすくなるという話になります.
今回の結果を確認してみましょう.
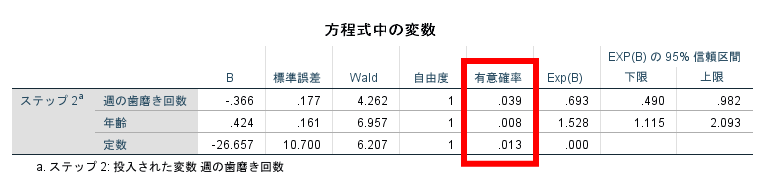
まずオッズ比を確認する前に各変数の有意確率を確認しましょう.
この変数の有意確率が5%未満でなければオッズ比も意味を持ちません.
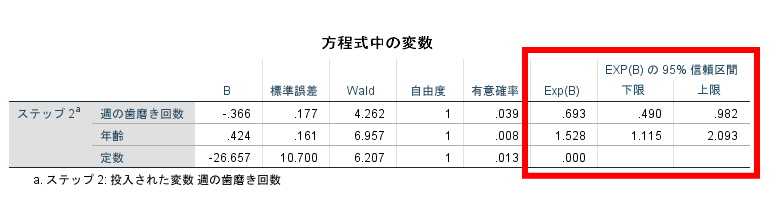
次にオッズ比を確認します.
オッズ比は1の時には全く影響がないことを意味し,1より大きいほどまたは小さいほど影響力が強いことになります.
今回の結果の場合には,週の歯磨き回数のオッズ比が0.693ですので週の歯磨きの回数が1回増えると0.693倍虫歯になりにくくなる.
つまり虫歯になる確率が7/10くらいになるという解釈ができます.
また年齢のオッズ比は1.528ですので1歳年齢を重ねると1.528倍虫歯になりやすくなるということになります.
ちなみにExp(B)の右側の数字はオッズ比の95%信頼区間です.
オッズ比が95%の確率でどの範囲にあるかを表したものです.
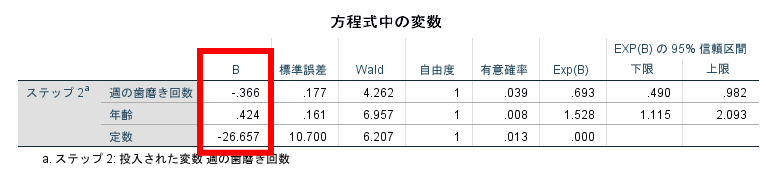
Bは偏回帰係数を表します.
論文や学会発表ではこの偏回帰係数(B)を記載する必要があります.
偏回帰係数は変数間の単位が異なると単純に比較できませんのであまり数字には大きな意味はありませんが,ロジスティック回帰モデルを作成する際にはこの係数が必要となります.
また今回のロジスティック回帰モデルでは最終的に2つの独立変数(週の歯磨き回数・年齢)が抽出されております.
今回のデータのサンプルサイズは30ですが,下記の基準を考慮してもサンプルサイズは適切だと考えてよいでしょう.
サンプルサイズ≧2×独立変数の数(Trapp, 1994)
サンプルサイズ≧3~4×独立変数の数(本多, 1993)
サンプルサイズ≧10×独立変数の数(Altman, 1999)
多重ロジスティック回帰分析の適合度を判定する指標
上述したようにモデルχ2値を用いてロジスティック回帰モデルを用いて回帰モデルの有意性を検討することができます.
ただ有意性の検定ではあくまでモデルが意味を持つかどうかを検討したにすぎず,モデルの適合度については明らかになりません.
そのため作成したモデルの精度を評価する指標として適合度を参照することが重要となります.
適合度を表す指標としてはHosmer-Lemeshow検定(ホスマー・レメショウ検定)や判別適中率を参照します.
Hosmer-Lemeshow検定(ホスマー・レメショウ検定)

Hosmer-Lemeshow検定(ホスマー・レメショウ検定)は回帰式の適合性の検定で実測値と予測値を比較する検定です.
Hosmer-Lemeshow検定(ホスマー・レメショウ検定)における有意確率が5%以上であれば適合度は良好と判断してよいでしょう.
5%未満であれば適合度は不良ということになります.
この場合には有意確率が0.376ですので適合度は高いと考えてよいでしょう.
正判別率
Hosmer-Lemeshow検定(ホスマー・レメショウ検定)と合わせて正判別率も確認しておきましょう.
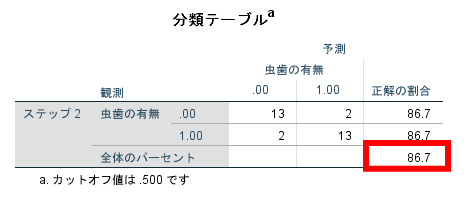
正判別率の明確な基準は存在しませんが,この場合には86.7%ですのでおおよそ8割以上はロジスティック回帰式によって虫歯の有無を判別できるということになります.
ロジスティック回帰式の有意性が確認できても回帰式の適合度が低いと回帰モデルは役に立つとは考えにくいので,別の独立変数を加えるなどの対応が必要でしょう.
その他にもAICやBICといった適合度の基準が存在しますが,基本的にはHosmer-Lemeshow検定(ホスマー・レメショウ検定)と正判別率の確認で十分です.
論文への記載方法
多重ロジスティック回帰分析の結果を論文に記載する際には以下の点をおさえておくとよいでしょう.
多重共線性の確認を行ったか,行った場合にはその手順
変数選択にはどの方法を用いたか(変数増加(減少)法:尤度比等)
適合度の評価は何を指標としたか
残差,外れ値の検討したか,行った場合はその手順
論文への記載例
従属変数を虫歯の有無,独立変数を性別・年齢・週の歯磨きの回数・歯磨き時間として二項ロジスティック回帰分析を行った.
独立変数の投入にあたっては事前に相関行列を作成し,独立変数間にr>0.80となる粗強い相関関係がないことを確認した.
尤度比による変数増加法による多重ロジスティック回帰分析の結果は以下の表のとおりであった.

モデルχ2検定の結果はp<0.05であり,各変数も有意であった.
ホスマー・レメショウ検定の結果はp=0.376であり,判別適中率も85.8%とモデルの適合度も良好であった.
なお実測値に対して予測値が±3SDを超えるような外れ値は存在しなかった.






コメント
[…] SPPSによる多重ロジスティック回帰分析の結果の見方をわかりやすく解説 … SPSSを使って統計解析をお手伝いします スポンサーリンク スポンサーリンク 未分類 シェアする Twitter Facebook LINE コピー spss-statistics2020をフォローする spss-statistics2020 素人でもわかるSPSS統計 […]
卒業論文の制作をしているものです。
二項ロジスティック回帰分析を用いて
「12点満点の既存尺度をカットオフポイントで分けて二値化したもの」を目的変数にし、
説明変数には、
「Aに関する10段階の自己評価」、「Bに関する10段階の自己評価」、「Cに関する10段階の自己評価」の項目を投入したいのですが、
分析にかけて結果を見ると
B 標準誤差 Wald ・・・
「Aの(1)」
「Aの(2)」
「Aの(3)」
・・・
「Bの(1)」
「Bの(2)」
「Bの(3)」
・・・
というように、各自己評価の項目の内訳が個別に表示されるのですが、何が原因でしょうか。
A
B
C
とまとまりで分析結果を出力させたいとかんがえています。