SPPSによる多重ロジスティック回帰分析をわかりやすく解説 従属変数(目的変数)と独立変数(説明変数)って? 変数選択の方法は? 多重共線性は? 必要なサンプルサイズ(標本数・n数)は?
このページではSPPSによるロジスティック回帰分析をわかりやすく解説させていただきます.また
従属変数(目的変数)と独立変数(説明変数)について,尤度比検定・Wald(ワルド)検定による変数選択の方法についても解説いたします.
また多重共線性や,ロジスティック回帰分析を行うに当たって必要なサンプルサイズ(標本数・n数)についても解説いたします.
多重ロジスティック回帰分析の特徴
多重ロジスティック回帰分析は簡単に言うと従属変数(目的変数)が2値のデータ(0-1データ)の場合の重回帰分析と考えるとわかりやすいと思います.
従属変数である2値のデータに関連する要因を抽出する場合に用いられます.
多重ロジスティック回帰分析の利点はデータの型や分布に厳密さを必要としないといった点です.
重回帰分析は厳密にいえば間隔・比率尺度のデータにしか適用できませんし,残差が正規分布する必要があるといった条件がありましたが,多重ロジスティック回帰分析にはこういった条件はありません.
よってより広い範囲のデータに使用しやすい検定と言えるでしょう.
多重ロジスティック回帰分析の概要
従属変数yに対して独立変数xの影響度合いを解析する
従属変数yの予測式を構築する
従属変数は質的(0-1データ)かつ1つ
独立変数は量的または質的変数で2つ以上
多重ロジスティック回帰分析の解析を行うまでの流れ
①従属変数と独立変数の選択
②多重共線性の確認
③独立変数選択の方法の決定
基本的には以上がロジスティック回帰分析を行うまでの流れです.
①従属変数と独立変数の決定
まずは従属変数と独立変数を選択します.
従属変数である2値のデータを決定した上で,独立変数を選択しますが,特に問題になるのが独立変数の決定方法です.
基本的に独立変数は2つ以上となりますが,独立変数が多い時には多重ロジスティック回帰分析を行う前に単変量解析(2群の比較)を行って投入する独立変数を絞り込んでおく必要があります.
ただし注意が必要なのはこの単変量解析(2群の比較)で従属変数と有意な関連を認めた変数を独立変数にすればよいという話ではありません.
単変量解析(2群の比較)で有意とならないにもかかわらずロジスティック回帰分析では有意となる場合もありますし,その逆もあり得ます.
したがって一般的な5%未満といった有意水準ではなく,明らかに有意水準からかけ離れた(p>0.25)のような変数を除外するといった方法が望ましいでしょう.
また場合によっては有意確率が0.25以上であっても専門的見地から考えると交絡因子として必ず含めた方が良い変数もあり得ると思います.
したがって投入する独立変数を決定する場合には,単変量解析(2群の比較)の結果は絶対的なものではなく参考程度に考えることが重要です.
標本の大きさと独立変数の数の考慮 必要なサンプルサイズ(標本数・n数)は?
ロジスティック回帰分析をはじめとする多変量解析では独立変数の数に対する標本の大きさ(サンプルサイズ=データの数)が重要となります.
サンプルサイズに対して独立変数の数が大きいとロジスティック回帰モデルの精度が悪くなってしまいます.
どのくらいのサンプルサイズが必要かについては明確な基準は存在しませんが一般的には以下のような基準を参照すると良いでしょう.
サンプルサイズ≧2×独立変数の数(Trapp, 1994)
サンプルサイズ≧3~4×独立変数の数(本多, 1993)
サンプルサイズ≧10×独立変数の数(Altman, 1999)
サンプルサイズ≧200(Kline, 1994)
この場合の独立変数の数というのは投入する独立変数の数ではなく,最終的に抽出された独立変数の数であるといった点にも注意が必要です.
②多重共線性の確認

多重共線性って何なの?

多重共線性というのは独立変数間の関連性が高すぎる場合に起こる様々な問題を指します.一般的には独立変数間に相関係数が1に近い関連性がある場合や,独立変数の個数が標本(データ数)の大きさに比べて大きい時に生じることがあります

多重共線性があるかをどうやって判断したらいいの?

多重共線性の有無を判断するには相関分析を行う必要があります
①独立変数間の相関行列から相関係数が1に近い変数が無いかを観察する
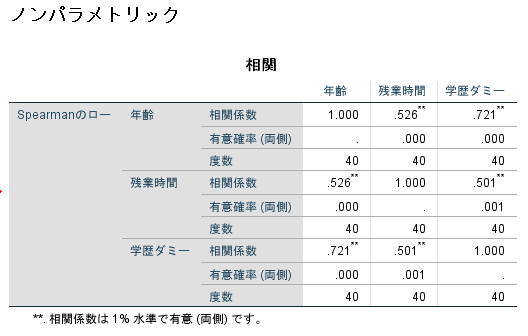
ここでは3つの独立変数間の相関に関してSpearmanの順位相関係数を用いて検討しましたが,rが0.80をこえる関連性は見られませんでした.
多重共線性を判断する場合にどの程度相関係数が高いと問題なのかについては明確な基準は存在しませんが,r>0.80が1つの基準になるでしょう.
ちなみに独立変数間にr>0.80となる高い関連性を有する独立変数が存在する場合には,どちらか一方の独立変数を削除するのが一般的です(専門的見地から考慮した上で削除することが重要です).
なお重回帰分析ではVIFのような指標を用いて多重共線性の判断が可能でしたが,ロジスティック回帰分析ではこのような多重共線性を判断するための指標は出力されませんので相関行列表を用いて多重共線性を確認する必要があります.
③独立変数選択の方法の決定
SPSSによるロジスティック回帰分析の場合には変数の選択方法として以下の方法があります.
強制投入法
変数増加(減少)法:尤度比
変数増加(減少)法:Wald
変数増加(減少)法:条件付
強制投入法
強制投入法は解析者が任意に独立変数を決めて解析する方法です.
どうしてもこの変数はモデルに含めたいといった場合には強制投入法を選択することもあります.
変数増加(減少)法:尤度比
変数増加(減少)法:尤度比は変数選択の基準として最も望ましい方法です.
特にこだわりが無ければ変数増加(減少)法:尤度比を選択しておけば間違いないでしょう.
尤度比検定というのは最大対数尤度を利用して回帰式を検定する方法です.
個々の独立変数の有意性を確認するというよりは回帰式全体の有意性を確認するといったイメージです.
変数増加(減少)法:Wald
Waldは各独立変数の有意性を基準に選択していく方法です.
Wald検定というのはオッズ比の信頼区間の退出に用いられる検定です.
このWald検定の特性として回帰係数の絶対値が大きくなると推定標準誤差が大きくなるために,Wald統計量は極めて小さくなるといった性質があります.
こういった問題を考えると変数増加(減少)法:尤度比を用いることが望ましいと考えられます.
SPSSを用いた多重ロジスティック回帰分析の実際
ここでは高齢者の虫歯の有無に影響を与える要因を明らかにする例をもとにSPSSを用いたロジスティック回帰分析の方法についてご紹介させていただきます.
従属変数:虫歯の有無
独立変数:性別・年齢・週の歯磨き回数・歯磨き時間
①分析⇒回帰⇒二項ロジスティック回帰分析を選択
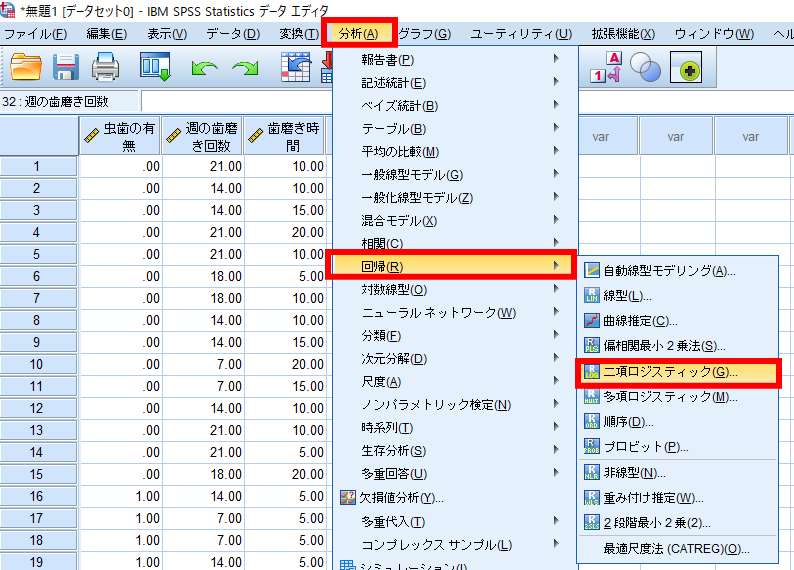
②従属変数と独立変数を決定
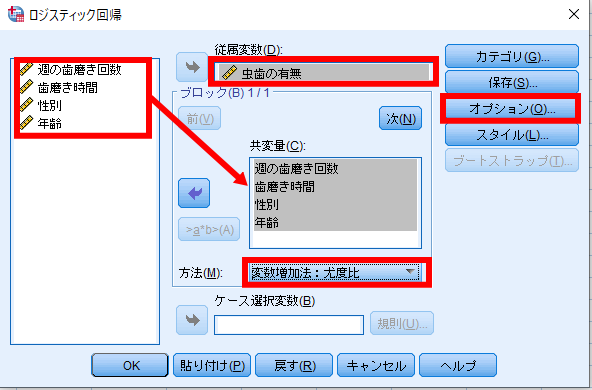
虫歯の有無を従属変数へ移動させます.
週の歯磨き回数・歯磨き時間・性別・年齢を共変量へ移動させます.
最後にカテゴリをクリックします.
③オプション変数の定義
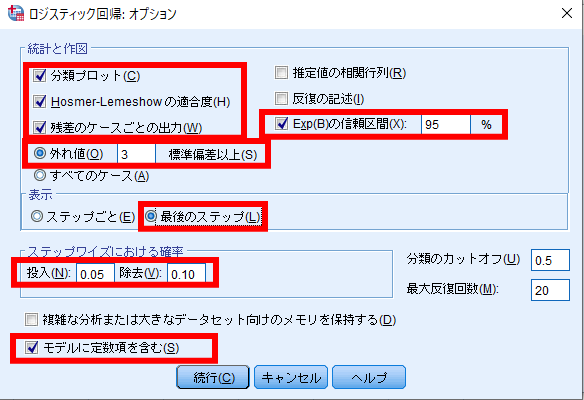
分類プロット・Hosmer-Lemeshowの適合度・残差のケースごとの出力にチェックを入れます.
外れ値にチェックを入れ,3標準偏差以上と入力します(デフォルト設定では2標準偏差となっております).
Exp(B)の信頼区間にチェックを入れ95%信頼区間となっているのを確認します.
モデルに定数項を含むにチェックがついていることを確認します.
結果の見方については後編で解説させていただきますので後編をご参照ください.







コメント
[…] SPPSによる多重ロジスティック回帰分析をわかりやすく解説 従属変数(目… […]