- 検者間信頼性・検者内信頼性とは?
- 級内相関係数(ICC:Intraclass correlation coefficients)とは?
- 級内相関係数(ICC:Intraclass correlation coefficients)にはCase1,Case2,Case3の3パターンが存在する
- ICC(2, 1)・ICC(2, k)とICC(3, 1)・ICC(3, k)の違いは?
- SPSSによる検者内信頼性・検者間信頼性・級内相関係数(ICC:Intraclass correlation coefficients)の求め方の実際
- カッパ(κ)係数とは?
- SPSSによるカッパ(κ)係数の算出方法
- 級内相関係数(ICC)やカッパ(κ)係数の判定基準
- 級内相関係数(ICC)の範囲制約性
検者間信頼性・検者内信頼性とは?
ある測定を2回以上繰り返した場合に,その測定方法が信頼できるのか,再現性(信頼性)がどのくらいかということを調べたいとします.
この場合には,平均の差を比較したり,相関を指標とするのも1つの方法です.
信頼性の指標として,近年では級内相関係数(ICC:Intraclass correlation coefficients)・カッパ係数といった信頼係数を算出することが多いです.
このページではSPSSを使った級内相関係数(ICC:Intraclass correlation coefficients)・カッパ係数の算出方法について解説させていただきます.
級内相関係数(ICC:Intraclass correlation coefficients)とは?
ある測定の検者間または検者内信頼性の指標として用いられるのが,級内相関係数(ICC:Intraclass correlation coefficients)です.
級内相関係数(ICC:Intraclass correlation coefficients)には以下のような適応条件があります.
正規分布に従うデータであること
比率尺度化間隔尺度,また一部例外として段階数の多い順序尺度のデータ
級内相関係数(ICC:Intraclass correlation coefficients)を算出する場合には,分散分析の結果を利用しますので,分散分析の適応条件である以下の条件を満たすことが理想となります.
1.データが無作為抽出である
2.データが正規分布に従う
3.各要因の水準間で等分散性が保証されている
このうち1・2の条件は必須となります.
級内相関係数(ICC:Intraclass correlation coefficients)にはCase1,Case2,Case3の3パターンが存在する
級内相関係数(ICC:Intraclass correlation coefficients)はCase1,Case2,Case3の3パターンに大別され,さらにそれぞれ2つの公式が存在します.
そのためICCは大きく分類すると6つに分類されます
Case1:ICC(1, 1)
Case1:ICC(1, k)
Case2:ICC(2, 1)
Case2:ICC(2, k)
Case3:ICC(3, 1)
Case3:ICC(3, k)
Case1は検者内信頼性を表します.
ICC(1,1)やICC(1,k)と表記します.
Case2は検者間信頼性を表します.
ICC(2,1)やICC(2,k)と表記します.
Case3も検者間信頼性を表します.
ICC(3,1)やICC(3,k)と表記します.
一般的にICC(1,1),ICC(2,1),ICC(3,1)は,検者内・検者間信頼性がどれくらいあるのかを知るために使用します.
これに対してICC(1,k),ICC(2,k),ICC(3,k)は,複数回測定した平均値を使用したときの検者内・検者間信頼性を求めるときに使用します.
例えばICC(1, 3)であれば3回測定した際の平均値の検者内信頼性を求めることになりますし,ICC(2, 3)であれば3名の検者が測定した際の平均値の検者間信頼性を求めることになります.
ICC(2, 1)・ICC(2, k)とICC(3, 1)・ICC(3, k)の違いは?
Case2とCase3の違いは,Case2は絶対一致を調べるもので,Case3は相対一致を調べるものです.
絶対一致と相対一致の相違については難解な内容ですが,検者が特定されているときの検者間信頼性を表すのがICC(3, 1)やICC(3, k)です.
一方でICC(2, 1)やICC(2, k)は想定した母集団からの検者であれば誰でもよいわけです.
つまり検者A・B・Cの3名が測定を行った場合に,検者3名の検者間信頼性を明らかにしたい場合には,Case2であるICC(2, 1)やICC(2, k)を,特定の検者Aの検者間信頼性を明らかにしたい場合には,Case2であるICC(3, 1)やICC(3, k)を使用することとなります.
SPSSによる検者内信頼性・検者間信頼性・級内相関係数(ICC:Intraclass correlation coefficients)の求め方の実際
検者内信頼性 Case1:ICC(1, 1)・Case1:ICC(1, k)
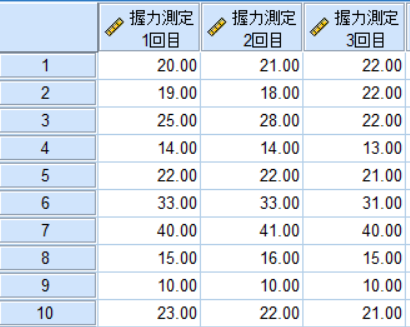
例えば同一の検者が握力を3回測定したとします.
この場合に,検者内の信頼性を求めます.
①正規性の検定(Shapiro-wilk検定)
上述したように級内相関係数を算出するうえではデータに正規性があることが条件となりますので,正規性の検定(Shapiro-wilk検定)を用いてデータの正規性を確認します.

正規性の検定については上のリンクをご参照ください.
この場合には正規性の検定(Shapiro-wilk検定)を行うと以下のような結果となりました.
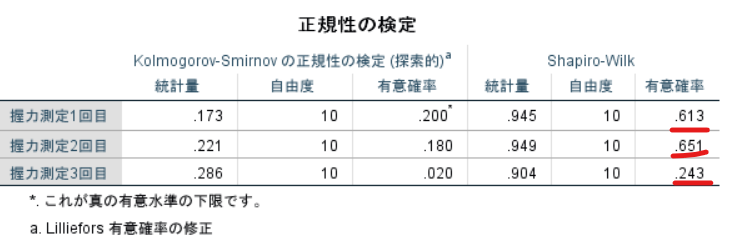
握力測定1回目・握力測定2回目・握力測定3回目いずれもShapiro-wilk検定における有意確率が5%以上ですので正規性が確認できました.
②ICC(1, 1)・ICC(1, k)の算出
メニューの分析⇒尺度⇒信頼性分析と選択します.
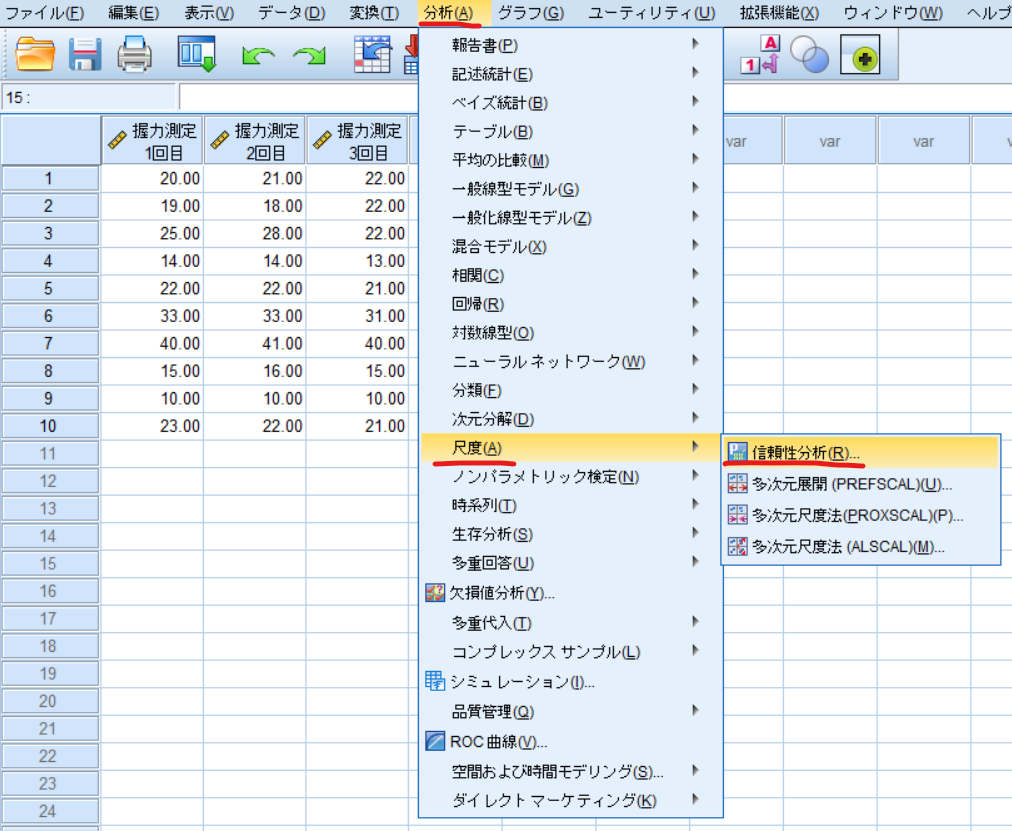
信頼性分析のダイアログボックスが立ち上がりますので,握力測定1回目・握力測定2回目・握力測定3回目のデータを項目に移動させます.
統計量をクリックします.
信頼性分析:統計量のダイアログボックスが立ち上がりますので,級内相関係数にチェックを入れたうえでモデルを一元配置変量を選択します.
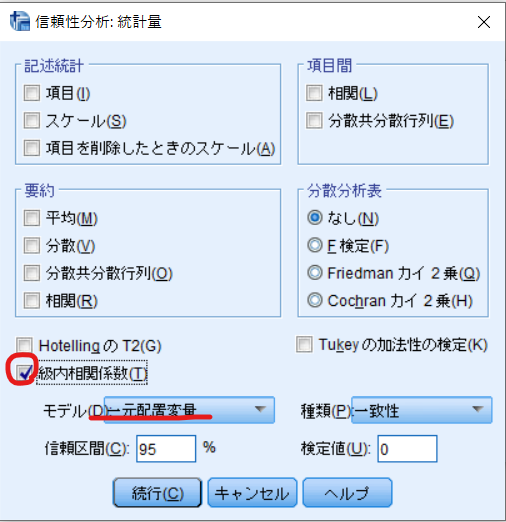
続行・OKとクリックすると以下のように級内相関係数が算出されます.
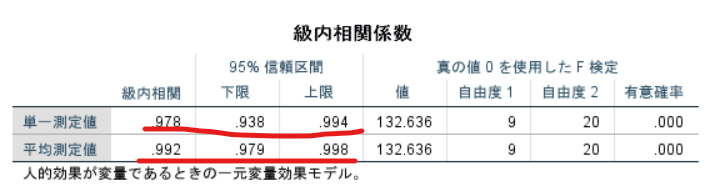
表中の単一測定値がICC(1, 1)を表します.
したがってこの表ではICC(1, 1)は0.978ということになります.
また表中の平均測定値がICC(1, k)を表します.
したがってこの表ではICC(1, k)は0.992ということになります.
級内相関係数に加えて確実におさえておきたいのが95%信頼区間です.
この場合にはICC(1, 1)の95%信頼区間は0.938~0.994ということになります.
つまりICC(1, 1)は95%の確率でICC(1, 1)は0.938~0.994のどこかにあるといった解釈ができます.
ICC(1, k)も同様に95%信頼区間をみると0.979~0.998であることがわかります.
この場合には3回測定を行っておりますので最終的には以下のように表記することになります.
ICC(1, 1)=0.978(0.938~0.994)
ICC(1, 3)=0.992(0.979~0.998)
検者間信頼性 Case2:ICC(2, 1)・Case2:ICC(2, k)
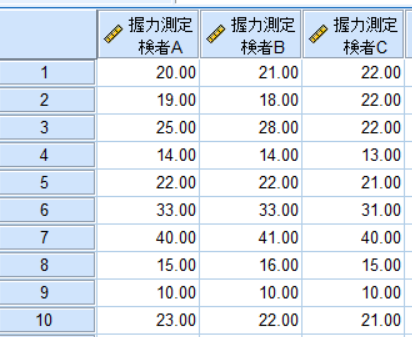
例えば異なる3名の検者が握力を3回測定したとします.
この場合に,検者間の信頼性を求めます.
①正規性の検定(Shapiro-wilk検定)
上述したように級内相関係数を算出するうえではデータに正規性があることが条件となりますので,正規性の検定(Shapiro-wilk検定)を用いて先ほどと同様にデータの正規性を確認します.
結果は先ほどと同様ですのでここでは省略させていただきます.
②ICC(2, 1)・ICC(2, k)の算出
メニューの分析⇒尺度⇒信頼性分析と選択します.
メニューの分析⇒尺度⇒信頼性分析と選択します.

信頼性分析のダイアログボックスが立ち上がりますので,握力測定1回目・握力測定2回目・握力測定3回目のデータを項目に移動させます.


統計量をクリックします.

信頼性分析:統計量のダイアログボックスが立ち上がりますので,級内相関係数にチェックを入れたうえでモデルを二元配置変量,タイプを絶対一致を選択します.

続行・OKとクリックすると以下のように級内相関係数が算出されます.
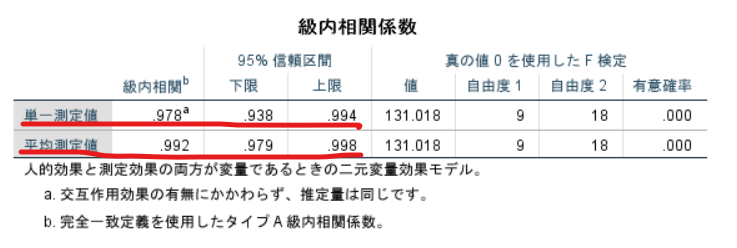
表中の単一測定値がICC(2, 1)を表します.
したがってこの表ではICC(2, 1)は0.978ということになります.
また表中の平均測定値がICC(2, k)を表します.
したがってこの表ではICC(2, k)は0.992ということになります.
級内相関係数に加えて確実におさえておきたいのが95%信頼区間です.
この場合にはICC(2, 1)の95%信頼区間は0.938~0.994ということになります.
つまりICC(2, 1)は95%の確率でICC(2, 1)は0.938~0.994のどこかにあるといった解釈ができます.
ICC(2, k)も同様に95%信頼区間をみると0.979~0.998であることがわかります.
この場合には3回測定を行っておりますので最終的には以下のように表記することになります.
ICC(2, 1)=0.978(0.938~0.994)
ICC(2, 3)=0.992(0.979~0.998)
Case3:ICC(3, 1)・Case3:ICC(3, k)
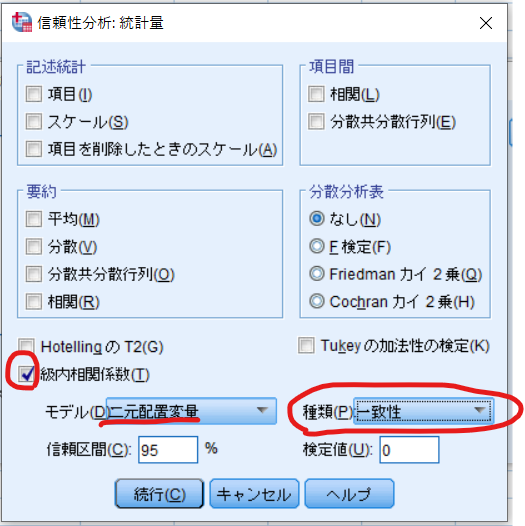
Case3についてはCase2とほぼ同様ですが,信頼性分析:統計量のダイアログボックスの操作が少し異なります.
信頼性分析:統計量のダイアログボックスが立ち上がりますので,級内相関係数にチェックを入れたうえでモデルを二元配置変量,タイプを一致性を選択します.
このタイプの選択がCase2と唯一異なるポイントです.
結果の見方もCase2と同様ですのでここでは省略させていただきます.
カッパ(κ)係数とは?
上述した級内相関係数が適応できるのは間隔尺度や比率尺度データまたは段階の多い順序尺度データに限られます.
これに対して名義尺度データや段階の少ない順序尺度データに適応されるノンパラメトリックの信頼性検定の手法がカッパ(κ)係数です.
カッパ(κ)係数は検者内信頼性も検者間信頼性も同一の方法で算出できます.
ICCと同様に0~1の範囲を取り,解釈方法もICCと同様です.
SPSSによるカッパ(κ)係数の算出方法
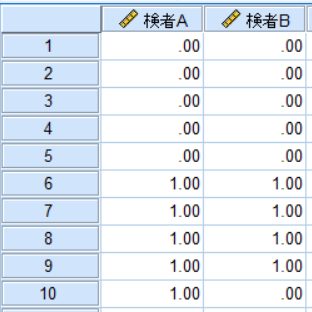
検者A・検者Bがある測定を行って陽性・陰性の判定を行ったとします.
この場合に陰性を0,陽性を1とし,検者間信頼性を検討した例を考えてみたいと思います.
分析⇒記述統計⇒クロス集計表と選択します.
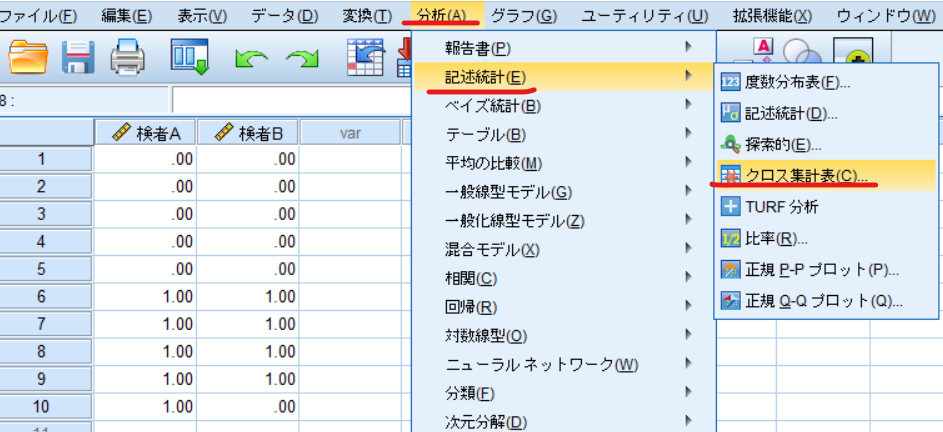
検者Aを行に検者Bを列に移動させます.
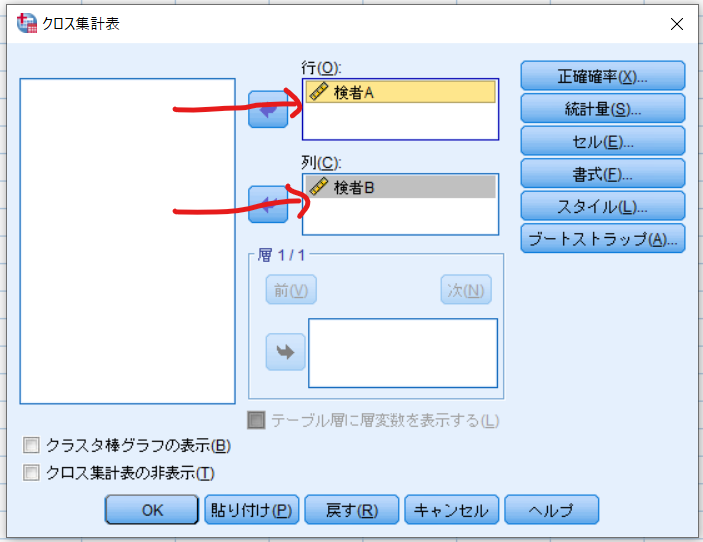
統計量をクリックします.
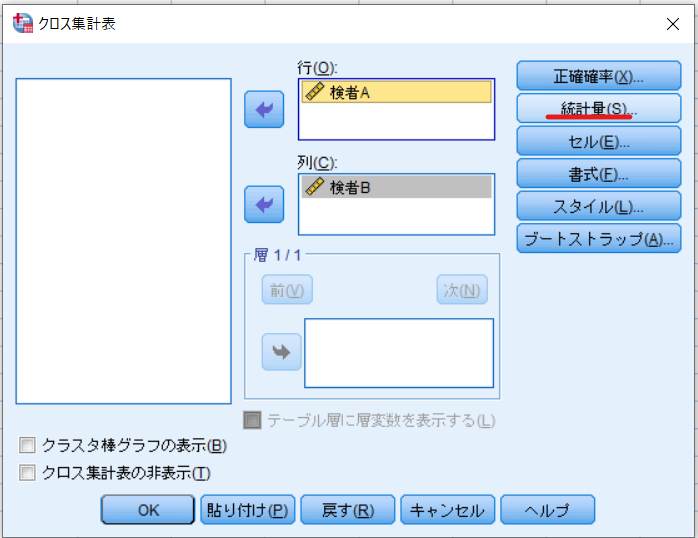
クロス集計表:統計量の指定ダイアログボックスが立ち上がりますので,カッパにチェックを入れて続行・OKで完了です.
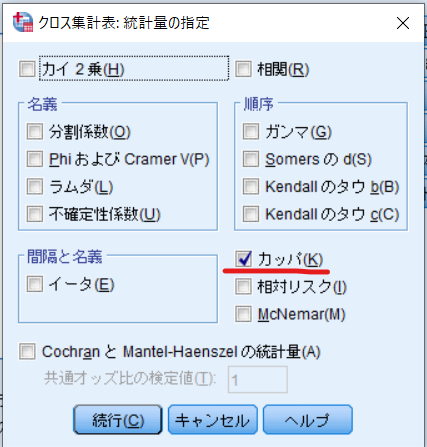
これがカッパ(κ)係数の結果です.

カッパ係数はこの場合0.800となります.
級内相関係数(ICC)やカッパ(κ)係数の判定基準
級内相関係数(ICC)やカッパ(κ)係数を算出したら以下のような判定基準をもとに判定を行います.
理論的な根拠は全くない基準ですのであくまで参考程度に考えた方がよいでしょう.
ICCの値のみならず95%信頼区間も含めて考慮することが重要です.
ICC=0.00-0.20⇒slight
ICC=0.21-0.40⇒fair
ICC=0.41-0.60⇒moderate
ICC=0.61-0.80⇒substantial
ICC=0.81-1.00⇒almost perfect
基本的にはICCやカッパ(κ)係数の95%信頼区間の下限値が0.70以上であれば最低限の信頼性は担保されると考えてよいでしょう.
級内相関係数(ICC)の範囲制約性
最後に少し難しい話を追加します.
級内相関係数の結果を解釈する際に注意が必要なのが範囲制約性の問題です.
ICCは被験者の個人差が大きいデータでは検者の個人差や誤差が想定的に小さくなって係数が大きくなるといった欠点があります.
例えば握力測定のICCを求める際に,握力が小さい被験者から大きい被験者まで幅広い握力値の被験者を対象とすると数値自体の再現性が低くてもICCは高くなります.
一方である握力値の範囲内の被験者のみを対象とするとICCは低くなる傾向があります.
こういった問題を信頼性の範囲制約性の問題と呼びますが,範囲制約性の問題に対しては標準誤差を算出して比較する方法などが報告されております.


