SPSSによる傾向スコア・マッチングの方法・手順は?(プロペンシティスコア)propensity score (PS) matchingキャリパーの設定方法は?
このページではSPPSによる傾向スコア・マッチングの方法や手順をわかりやすく解説させていただきます.
SPSSのケースコントロールの一致の機能を用いた傾向スコア・マッチングの方法について解説いたします.
またキャリパー(caliper)を傾向スコアの標準偏差の0.20倍とし,非復元抽出による1対1の最近傍マッチングを行う方法についても解説いたします.
SPSSを用いた傾向スコア・マッチングの必要性
ここでは運動介入の有無が健診結果と血糖コントロールの指標であるHbA1cに影響を与える要因を明らかにする例をもとにSPSSを用いた傾向スコア・マッチングの方法についてご紹介させていただきます.
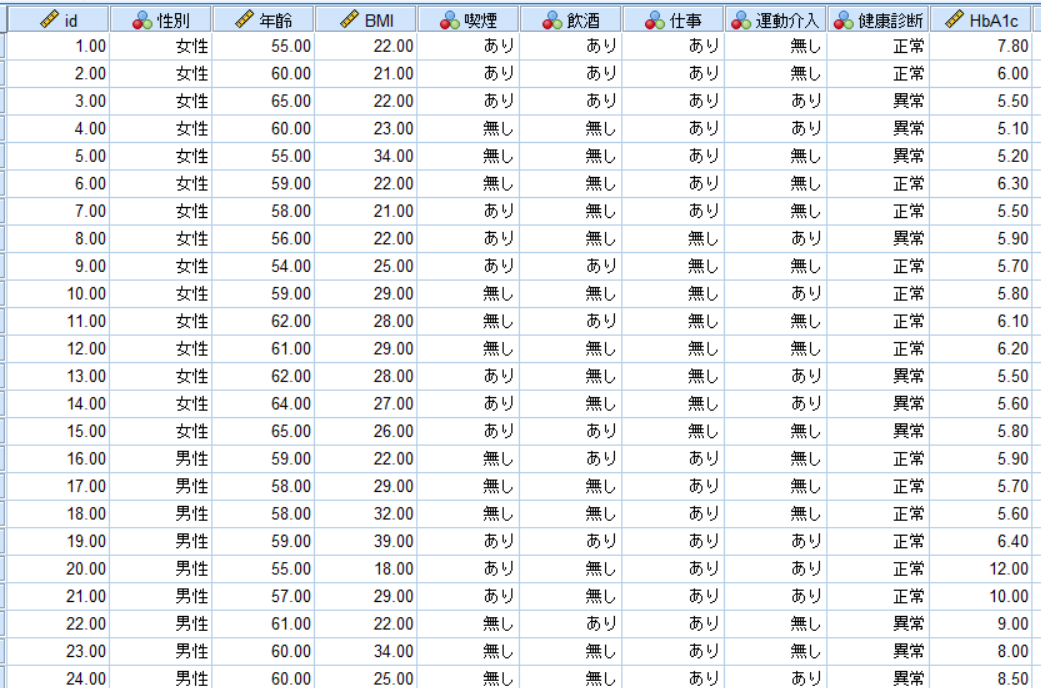
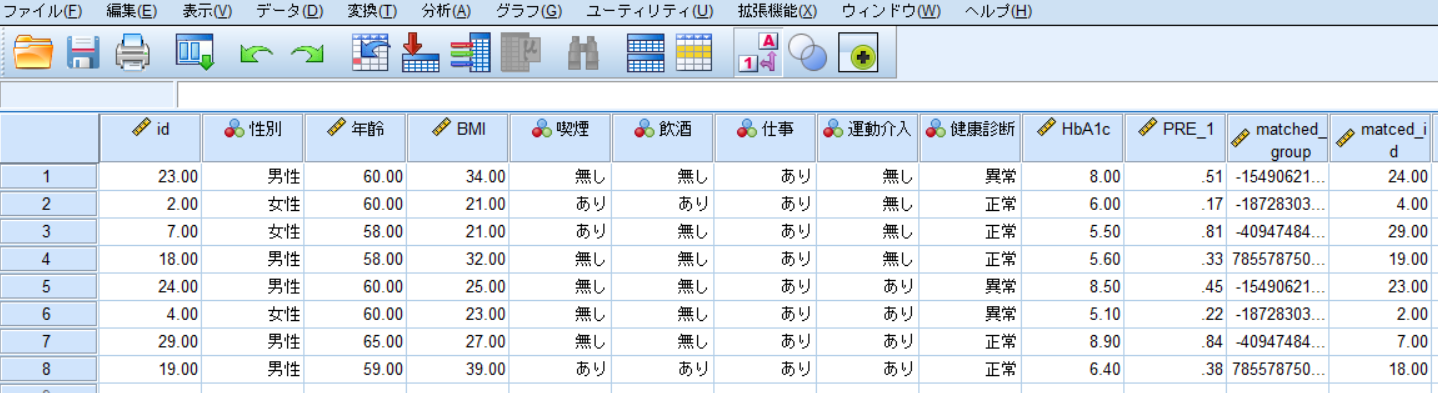
これが今回使用するデータです.
今回は運動介入の有無(運動介入の有無は無作為ではない)が健診結果やHbA1cに与える影響を検討するわけですが,健診結果やHbA1cに関連する要因としては,喫煙や飲酒習慣,仕事の有無や年齢などさまざまな要因が考えられます.
また運動介入を受け入れた対象は元来,健康意識が高い者が多いことが予測されますので,運動介入を行っている者ほど喫煙習慣を持つ者が少なかったり,BMIが正常値の者が多い可能性も考えられます.
つまりここでは運動介入を行う場合と行わない場合で「適応による交絡」が生じていると考えられます.
そのため単純に運動介入の有無で健診結果やHbA1cを比較することはできません.
「適応による交絡」を考慮したうえで健診結果やHbA1cを比較する必要があり,「適応による交絡」を考慮したうえで健診結果やHbA1cを比較するためには,傾向スコア・マッチングを使用する必要があります.
SPSSを用いた傾向スコア・マッチングの実際
①傾向スコア(プロペンシティスコア・propensity score (PS) )を算出するための独立変数の決定
はじめに傾向スコア(プロペンシティスコア・propensity score (PS) )を算出します.
傾向スコア(プロペンシティスコア・propensity score (PS) )を算出するうえで重要なのは運動介入の有無に関連しそうな交絡を可能な限りすべて含めることです.
傾向スコア・マッチングは決して万能な方法ではありません.
傾向スコア分析ではあくまで測定された交絡因子のみを制御しているにすぎませんので,未測定交絡因子によるバイアスには依然として晒されている点に注意を払う必要があります.
可能な限り運動介入の有無に関連しそうな交絡を可能な限りすべて含めたうえで傾向スコア(プロペンシティスコア・propensity score (PS) )を算出する必要があります.
ここでは以下の要因を投入して傾向スコア(プロペンシティスコア・propensity score (PS) )を算出します.
性別
年齢
BMI
喫煙
飲酒
仕事
②傾向スコア(プロペンシティスコア・propensity score (PS) )を算出
分析⇒回帰⇒二項ロジスティックと選択
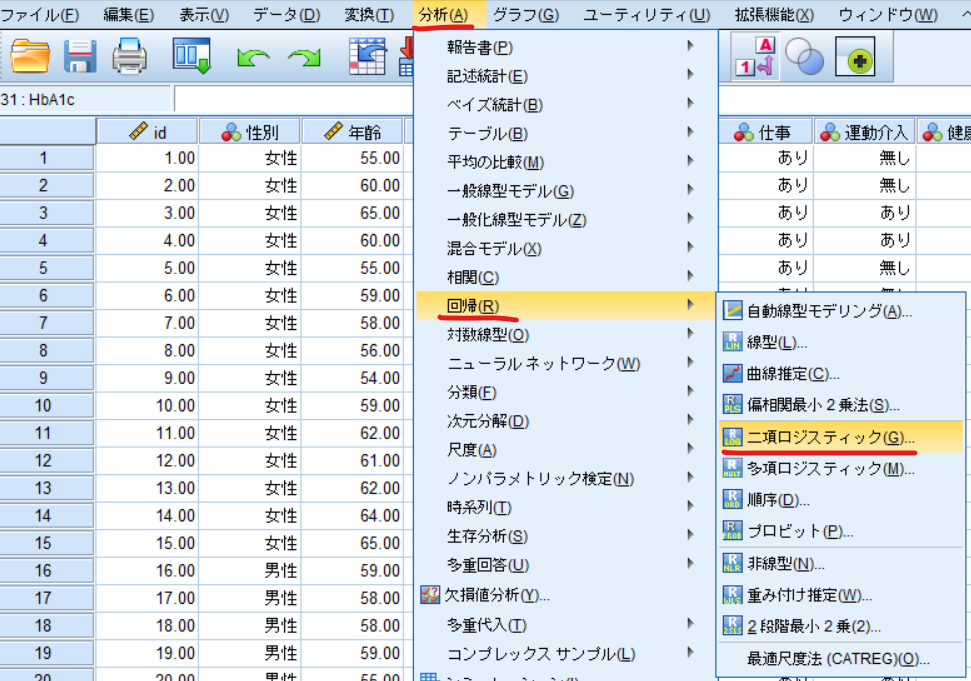
「運動介入」を従属変数へ,性別・年齢・BMI・喫煙・飲酒をブロックへ移動させます.
それからカテゴリをクリックします.
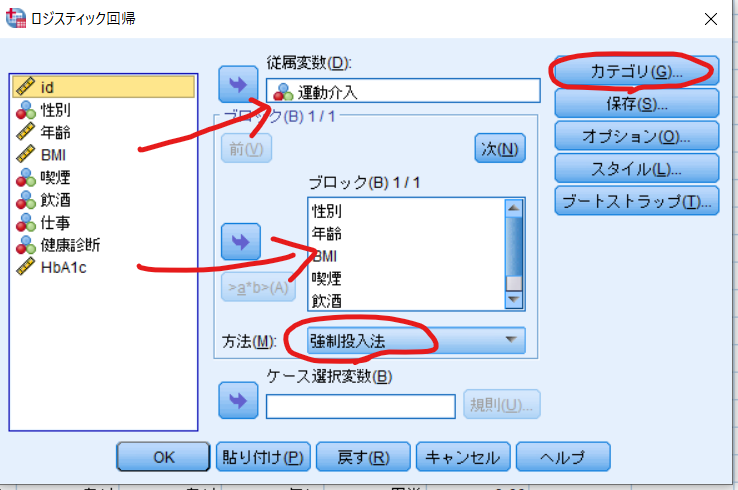
性別・年齢・BMI・喫煙・飲酒の中でカテゴリー変数のみをカテゴリ共変量へ移動させます.
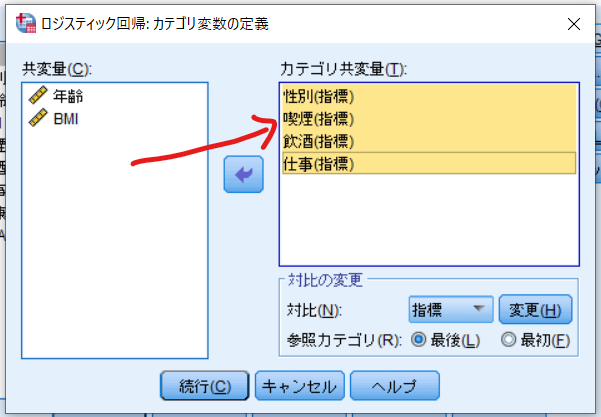
保存をクリックします.
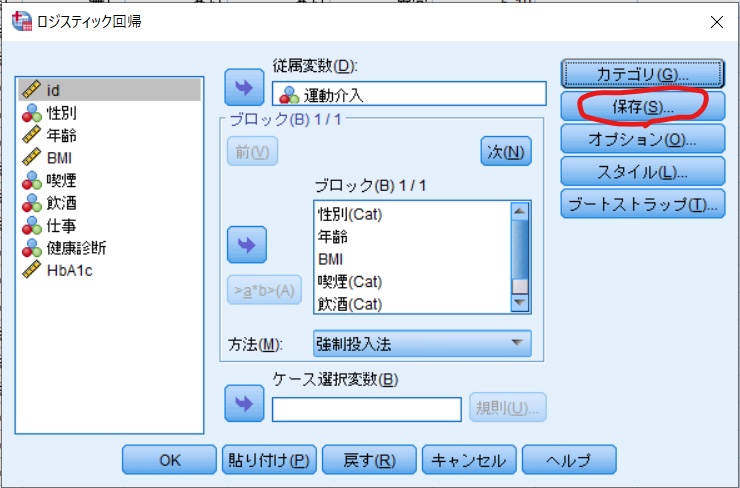
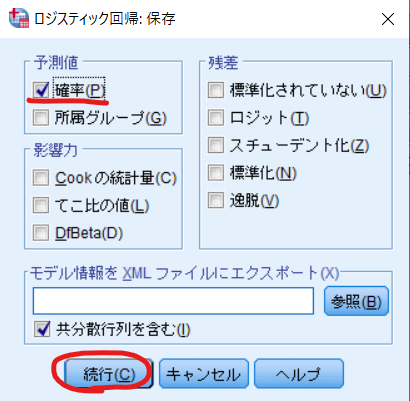
以下のようなダイアログが立ち上がりますので,確率にチェックを入れて続行をクリックします.
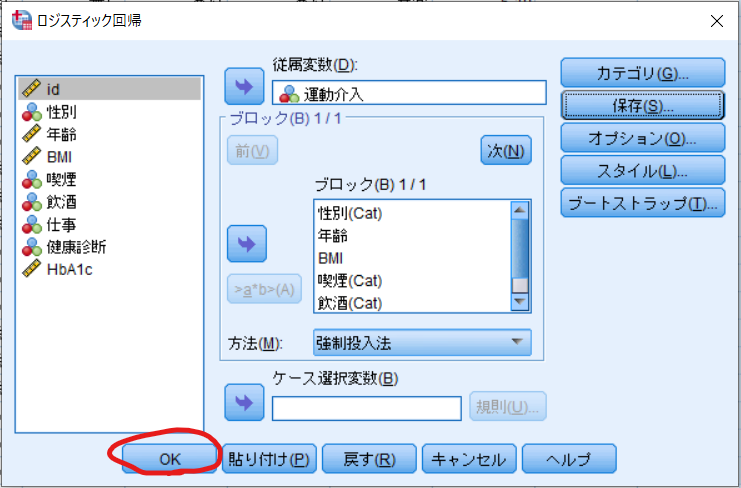
最後にOKをクリックして完了です.
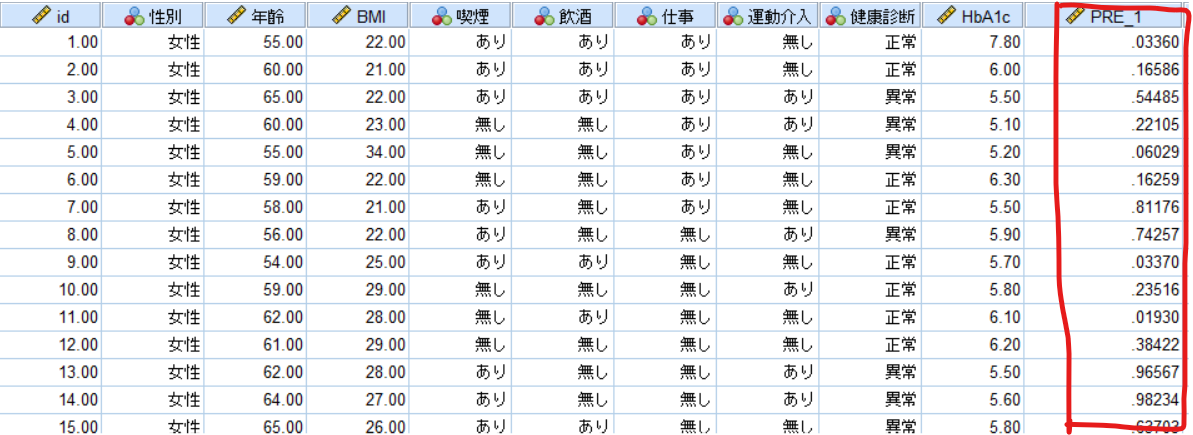
以下のように変数ビューにPRE_1という変数が出力されていれば成功です.
このPRE_1が傾向スコアになります.
③c統計量の算出の意義
傾向スコアを算出したら,傾向スコアが運動介入の有無をうまく識別できているかどうかを確認する必要があります.
運動介入の有無を状態変数(1または0)として,傾向スコア(PRE_1)を兄弟変数としたROC曲線を描き,曲線下面積(AUC:Area under the curve)を算出します.
このAUCがc統計量に相当します.
c統計量であるAUCは0.5≦AUC≦1.0となりますが,高すぎても低すぎてもよくありません.
一般的には
が理想です.
c統計量(AUC)が0.60未満の場合
c統計量(AUC)が0.60未満の場合には,傾向スコアによる運動介入の有無に関する識別能が低いことになりますので,そもそも傾向スコア・マッチングを行う意義が低くなってしまいます.
c統計量(AUC)が0.90以上の場合
またc統計量(AUC)が0.90以上の場合には,運動介入を行った群と運動介入を行っていない群のオーバーラップが少なく,マッチングされるペアが少なくなってしまい,多くのデータが除外されてしまいます.そのため統計学的な検出力が大きく低下してしまうことになります.さらに除外された症例が多くなると一般化可能性がも損なわれることになります.このような場合には運動介入を行った群と運動介入を行っていない群の適応が全く異なっていることになりますので,両者の効果の比較自体が意味を持たないことになってしまいます.
④c統計量の算出の実際
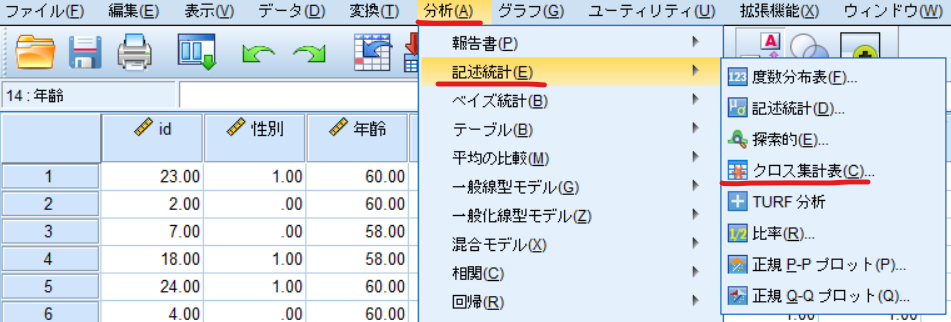
分析⇒ROC曲線と選択します
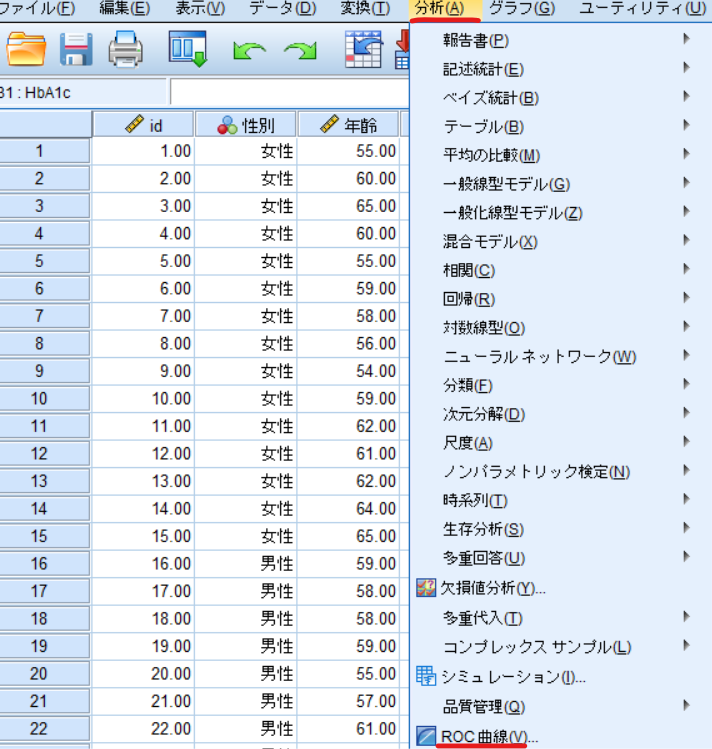
検定変数に予測確率(PRE_1)を移動させ,運動介入を状態変数に移動させます.
状態変数の値を1として表示のROC曲線・標準誤差と信頼区間・ROC曲線の座標点にチェックを入れます.
最後にOKをクリックします.
出力結果の中からAUCを参照します.
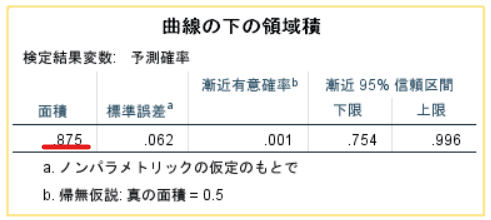
この場合にはAUCは0.875ですので,0.60<AUC<0.90でありますので,傾向スコア・マッチングを行うことの妥当性が確認できたと言えるでしょう.
⑤キャリパーの算出
傾向スコア・マッチングを行ううえではキャリパー値を設定する必要があります.
最近傍マッチングでは,ペアとして抽出される2つのデータの傾向スコアの差の絶対値が一定のキャリパー(閾値)の範囲内に収まるように設定する必要があります.
キャリパーは全対象者の傾向スコアの標準偏差の0.20倍に設定されることが多いです.
分析⇒報告書⇒ケースの要約と選択します.
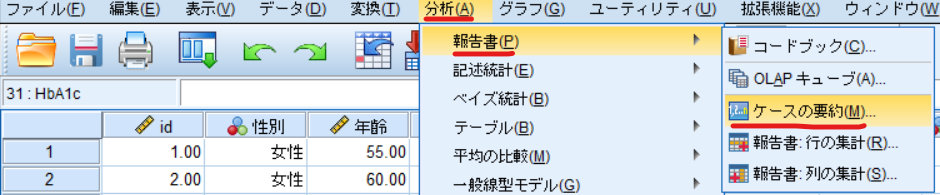
予測確率(PRE_1)を変数に移動させて統計量をクリックします.
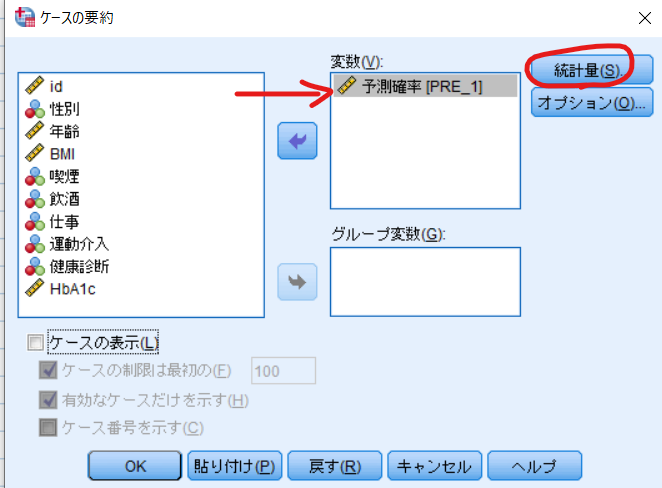
統計量の中から標準偏差をセル統計量に移動させて,続行,OKをクリックすれば傾向スコアの標準偏差が出力されます.
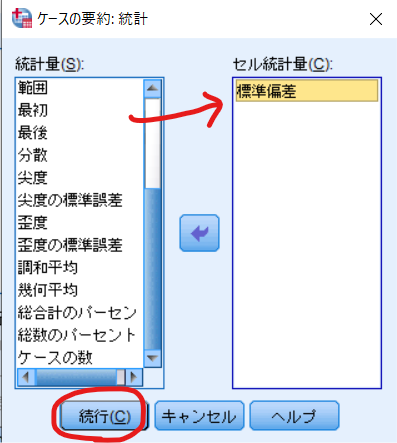
これが出力された標準偏差となります.

標準偏差は0.332ですので,0.20倍だとキャリパーは0.0664に設定すればよいということになります.
⑥マッチングの実行
データ⇒ケースコントロールの一致と選択します
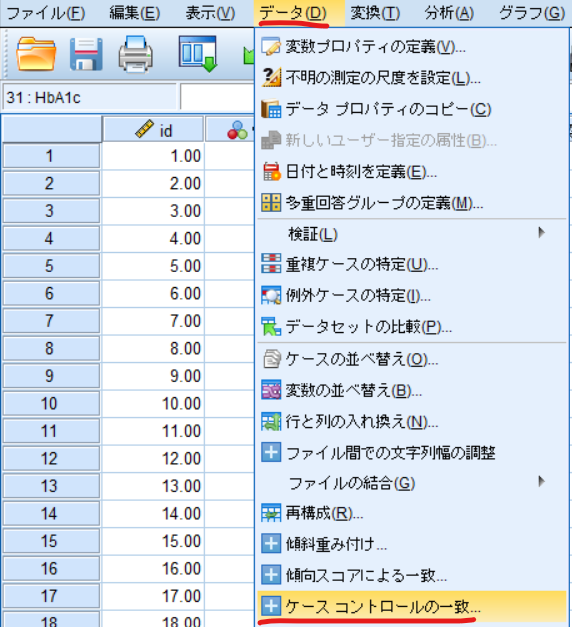
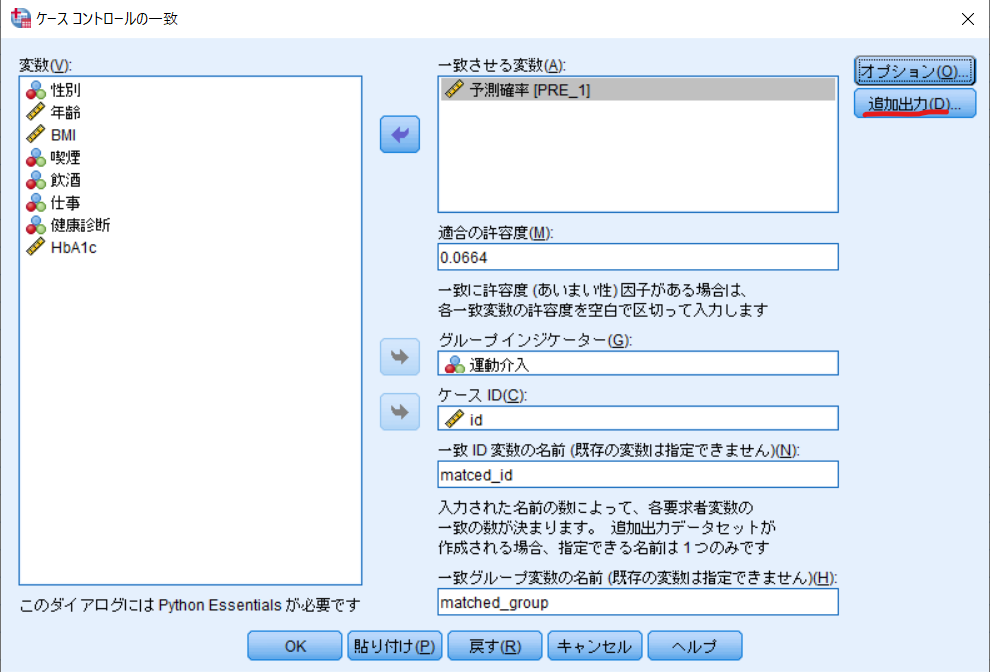
予測確率(PRE_1)を一致させる変数に移動させます.
適合の許容度はキャリパーの算出した傾向スコアの標準偏差は0.332の0.20倍の0.0664と入力します.
グループインジケーターは運動介入,ケースIDにはid(対象者毎のidを事前に設定しておく必要があります),一致ID変数の名前にmatched_id,一致グループ変数の名前にmatched_groupと入力します.
最後にオプションをクリックします.
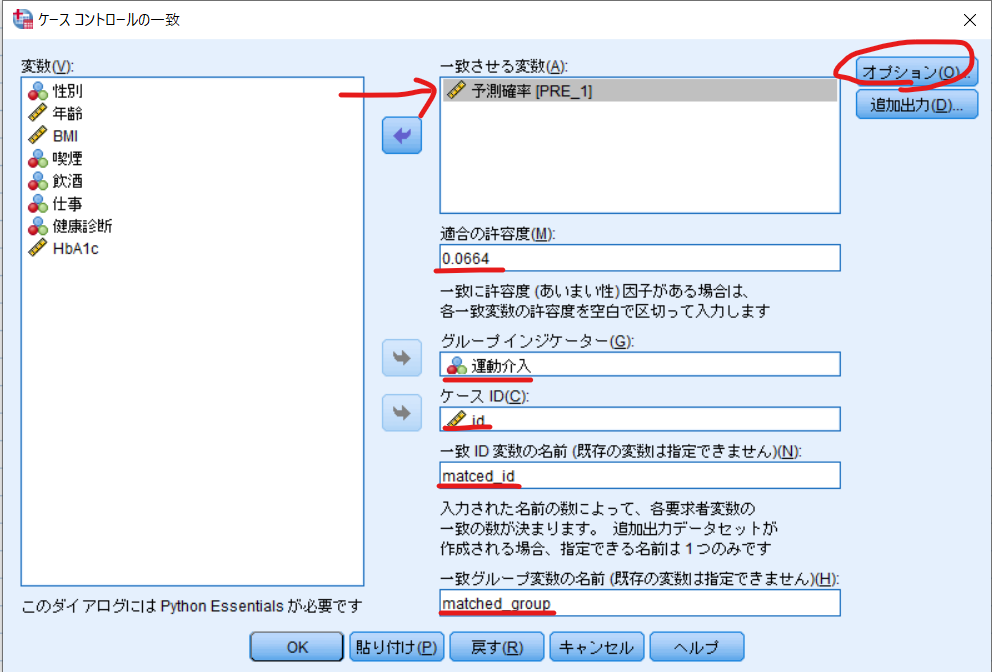
以下のように入力して続行をクリックします.
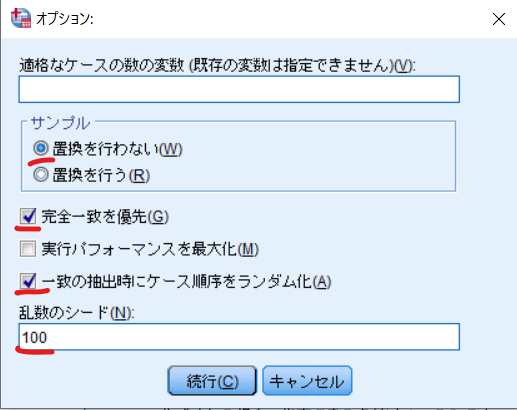
次に追加出力をクリックします.
追加出力データセットの作成にチェックを入れて,任意のデータセット名を入力して続行をクリックします.
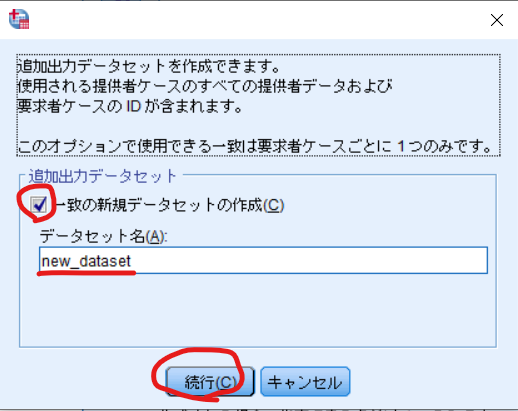
最後にOKをクリックすればマッチングの完了です.
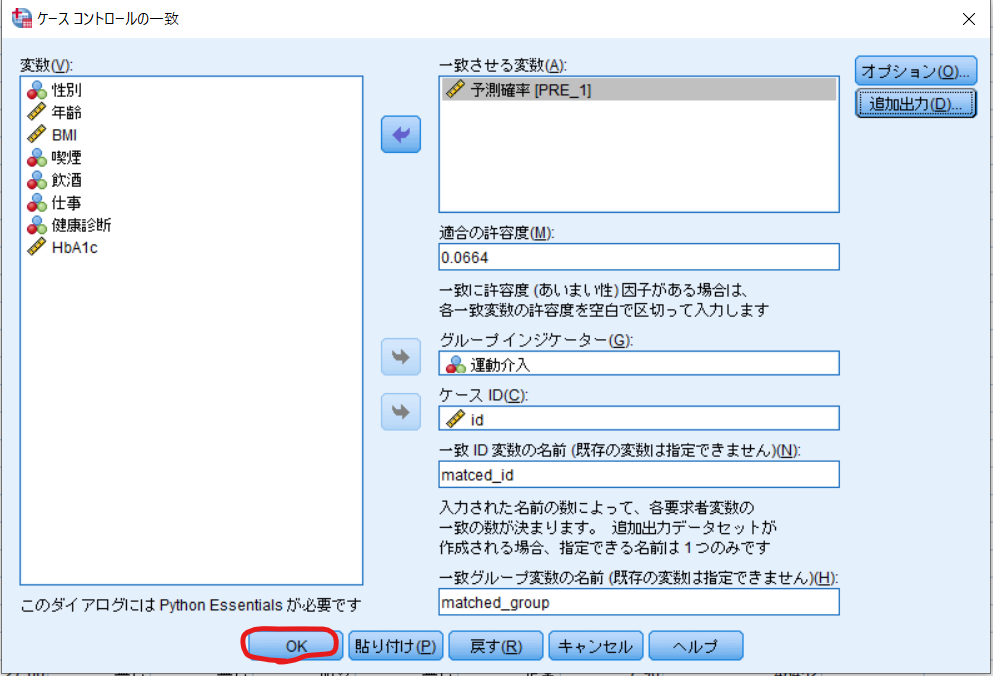
⑦マッチングデータの作成

既存のデータファイルに加えて新しいデータファイルが作成されます.
このデータが運動介入を行っていない(運動介入=0)データの中で,マッチングで最終的に残ったデータとなります.
一番右側のmatched_idというのがこのデータにマッチする運動介入を行っている(運動介入=1)のデータということになります.
今回は最終的に運動介入を行っていない(運動介入=0)データの中でidが23・2・7・18のデータに加えて,運動介入を行っている(運動介入=1)のデータの中でidが24・4・29・19のデータを用いて最終的に比較を行うということになります.
最後に一番左の列のidのデータと一番右の列のidのデータを抽出してマッチングデータセットを作成します.
こちらが最終的にできたマッチングデータセットになります.
今回は30例のデータからマッチされたデータは最終的に8例になったというわけです.
⑧マッチングデータを用いて比較
最終的にはマッチングデータを用いて運動介入の有無による比較を行います.
健康診断の結果はカテゴリカルデータですのでカイ2乗検定を用いて比較を行います.
詳しくはカイ2乗検定のページをご参照ください.

HbA1c結果は連続変数ですので正規性の検定を行ったうえで,対応のないt検定またはMann-WhitneyのU検定を用いて比較を行います.
詳しくは以下のページをご参照ください.



⑨対応のある検定を用いるか対応のない検定を用いるか?
上述したような方法でマッチング後に両群間のアウトカムを比較することになりますが,この場合に問題になるのが対応のある検定を用いるか対応のない検定を用いるかといった点です.
傾向スコア・マッチングではペアを考慮した検定を行うべき,すなわち今回の検定であればカイ2乗検定ではなくMcNemar検定を,対応のないt検定やMann-WhitneyのU検定ではなく,対応のあるt検定やWilcoxonの符号付順位和検定を用いるべきだといった考え方もあります.
しかしながら傾向スコアマッチングにおいてペアを考慮することがそれほど重要かどうかは現在のところ結論が出ておりません.
また実際のところペアを考慮してもしなくてもほとんどの場合には結果に差が無いこともわかっております.
そのため現在のところは対応のない検定を用いても間違いではないと言えるでしょう.



