サンプルサイズの計算がなぜ必要なのか?
統計学的検定を行う際には,サンプルサイズを決定することが重要となります.
なぜかというと統計学的検定というのは,仮に有意確率P値が0.05未満であっても,その結果が偶然ということもあり得るからです
統計学的検定には実はからくりがあって,サンプルサイズ(n数)が大きくなると,必然的にP値は小さくなります.
対応のあるt検定におけるt値は以下の数式で算出できます.
t値=√n(A群の平均値-B群の平均値)/標準偏差
t値が大きくなると値が小さくなりますので,t値が大きいほどt検定では有意差が出やすくなります.
この数式からどうすればt値が大きくなるかを考えてみると,以下のような3パターンが考えられると思います.
- 治療前と治療後の差を大きくする⇒2群の差が大きければ差が出やすい
- 標準偏差(SD)を小さくする⇒データのばらつきが小さければ差が出やすい
- サンプルサイズ(n)を大きくする⇒nが多ければ差が出やすい
このようにサンプルサイズが大きくなると,差が出やすくなってしまうわけです.

統計学的には有意差があってもnが大きいから差が偶然出るってことがあるの?

その通りです.本当に2群間に差があって有意差が出る場合もあれば,サンプルサイズが大きいために有意差が出るといった場合もあります.
したがって適切なサンプルサイズで統計学的な検定を行わないと,サンプルサイズが大きかったから有意差が出たということになってしまいます.
そのため通常は,事前にサンプルサイズを決定して必要なサンプルサイズを決定してから,研究を行うことが重要となります.
G*powerを用いて事前にサンプルサイズを決定するためは何が必要か?
サンプルサイズの計算がなぜ必要なのかについてはご理解いただけたかと思います.

サンプルサイズってどうやって決めればよいの?

サンプルサイズを決定するためには,3つの要因を決定する必要があります
- 1.効果量
2.αエラー
3.検出力(βエラー)
4.Allocation ratio(対応のあるt検定の場合には比較する群のサンプルサイズが同等なので,Allocation ratioは必然的に1になりますので入力する必要がありません)
ここからはこの3つの要因の決め方についてご説明いたします.
効果量にはいくつかの設定方法があります.
まずサンプルサイズを事前設計する(研究を行う前にサンプルサイズを決める)場合には,①先行研究における効果量を用いる方法,②予備調査における効果量を用いる方法,③中間解析データを用いる方法があります.
自身の研究と類似した研究があれば,類似した研究の効果量を用います.
対応のあるt検定の場合には効果量(d)が算出されていれば,その値を用います.
仮に効果量(d)が算出されていなければ,G*powerを用いて計算をします.

Test family⇒t testを選択
Statistical test⇒Means:Difference between two independent means(matched pairs)を選択(対応のないt検定の場合にはtwo groupsを選択)
Type of power analysis⇒A priori:Compute required sample size
Determineをクリックして効果量(d)を計算

①治療前の平均値を入力(この場合,50)
②治療後の平均値を入力(この場合,60)
③治療前の標準偏差を入力(この場合,5)
④治療後標準偏差を入力(この場合,5)
⑤治療前・治療後のデータの相関係数を入力
対応のあるt検定を使用しているということは正規性のあるデータということになりますので,パラメトリックの分布に使用する相関係数であるPearsonの積率相関係数を事前に算出しておく必要があります
⑥Calculateをクリック,効果量(d)=3.162を確認
⑧Calculate and transfer to main windowをクリック
これで効果量(Effect size d)のところに”3.162″と表示されるのが確認できます.
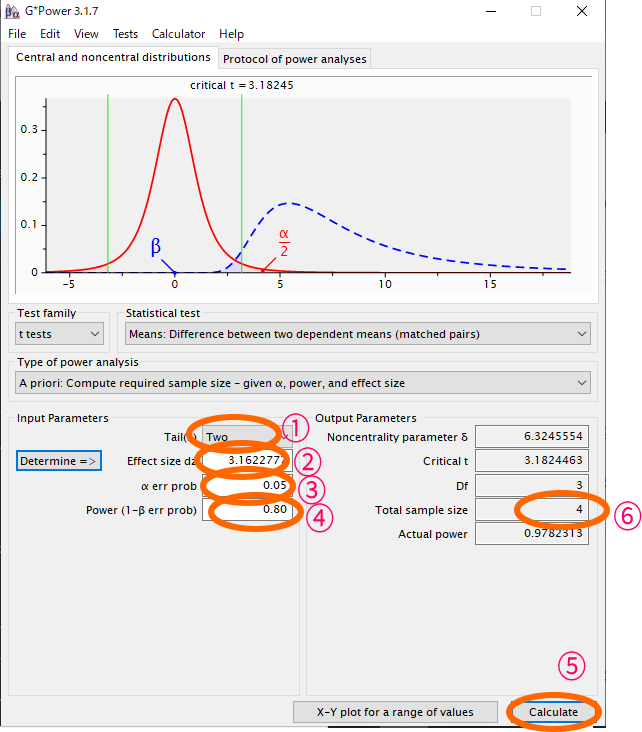
①one=片側検定,two=両側検定ですが,通常はtwoを選択
②効果量(Effect size d)のところに”3.162″の表示を確認
③αエラーを設定します.通常は0.05としますが,0.01でもかまいません
④検出力(1-βエラー)を設定します.デフォルト設定では0.95となっておりますが,0.8とされていることも多いです.通常はβがαの4~5倍になるように設定します.
⑤Calculateをクリック
⑤最終的に合計4例のサンプルサイズが妥当だといった結論が得られます.この場合には,4例で研究を終了して有意差が得られれば,n数が多すぎたから有意差が出たと指摘を受けずに済むわけです.
予備調査における効果量を用いる場合も基本的には先行研究における効果量を用いる方法と同様です.
予備調査における平均値や標準偏差を用いて効果量を算出した上で,サンプルサイズの設計を行います.
中間解析とはある程度,測定を行った段階で解析を行い,残りどのくらいのサンプルが必要かを検討する方法です.
中間解析における効果量を用いる場合も基本的には先行研究における効果量を用いる方法と同様です.
中間解析における平均値や標準偏差を用いて効果量を算出した上で,サンプルサイズの設計を行います.
最終的に算出されたサンプルサイズを目標に残りの調査を行うこととなります.
事前にサンプルサイズを設計できなかった場合には事後にG*powerを用いてサンプルサイズが適当だったか検出力を確かめよう

サンプルサイズって事前に決めるんでしょ?事後でも対応できるの?

サンプルサイズは事前に設計することが多いですが,事後にサンプルサイズが妥当であったかを調べる方法もあります.これを事後分析と呼びます
ここでG*powerを用いた事後分析の方法をご紹介いたします.

①Test family⇒t testを選択
②Statistical test⇒Means:Difference between two independent means(matched groups)を選択
③Type of power analysis⇒Post hoc:Coputed achieved powerを選択
④Tailsはtwo(両側検定)を選択
⑤効果量(d)を入力(効果量(d)を算出していない場合には,Determineをクリックして,平均値と標準偏差から効果量を算出.ここでは仮に”1.0″とします)
⑥αエラーを設定.通常は0.05としますが,0.01でもかまいません検出力(1-βエラー)を設定.
⑦研究におけるサンプルサイズを入力(ここではn=8とします)
⑧Calculateをクリック
⑨最終的に検出力が0.680と出力される(検出力が0.80を下回っているので,検出力はあまり高くないと判断できます).

事後分析の検出力って高ければいいの?

事後分析の検出力が1になっている場合には注意が必要です.検出力が1になっている場合には,サンプルサイズが過大な可能性が考えられます.つまりサンプルサイズが大きいために偶然差が出ている可能性があります.したがって検出力が0.80~1.00の値になることが理想です.




コメント
[…] フリーソフトG*powerを使った必要なサンプルサイズの計算(検出力分析・検… […]