偏相関分析の必要性
2変数の関係性を見る方法については,パラメトリックの検定であるPearson(ピアソン)の積率相関係数とノンパラメトリックの検定であるSpearman(スピアマン)の順位相関係数についてご紹介させていただきました.
今回は偏相関分析についてご紹介させていただきます.

偏相関分析ってどんな時に使うの?

偏相関分析はある変数とある変数の直線関係を他の変数の影響を取り除いて知りたい場合に使用します.ある変数とある変数に相関関係があっても,他の変数の影響を受けた,見かけ上の相関関係(擬似相関)が考えられる場合には,この他の変数の影響を除いた状態で変数間の関連性を分析する必要があります.
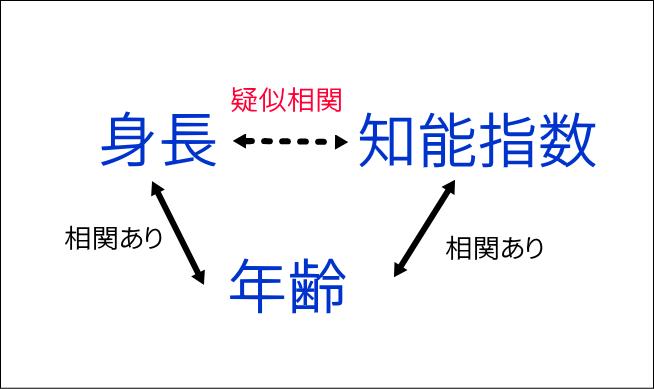
例えば小学生の身長と知能指数と年齢との関係について考えてみたいと思います.
まず小学生の身長と年齢に相関関係があることには異論はないと思います.
また小学生の知能指数と年齢にも相関があることには異論はないと思います.
では知能指数と身長ってどうでしょうか?
背が高いほど知能指数が高いと言われてもなんかしっくりこないと思います.
実は身長と知能指数は年齢といった交絡が介在することで疑似相関を呈しているのです.
つまり身長と知能指数に本当に関連があるかどうかは,身長と知能指数の相関関係を調べるだけではよくわからないということになります.
そのため身長と知能指数の間に本当に関連性があるかどうかを調べるためには,年齢を考慮した上で身長と知能指数との関連性を調べる必要があります.
こういった場合に用いられるのが偏相関分析です.
偏相関分析では年齢を考慮した上で身長と知能指数の間に関連性があるのかどうかを明らかにすることができます.
偏相関分析の適用条件
・正規分布に従うデータ(正規性の判断についてはコチラを参照してください)
・データが比率尺度データ・間隔尺度データ
(多段階の順序尺度のデータに対して用いることも可能です)
・対応のある3変数以上のデータ
SPSSを使用した偏相関分析-データ入力の方法-
SPSSで偏相関分析を算出する場合にはデータの入力方法は簡単です.
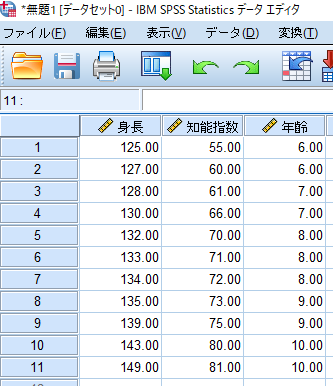
このように横列に関係性を分析したい同一対象者のデータと影響を取り除きたい制御変数(この場合には年齢)を並べます.
SPSSを使用した偏相関分析の方法
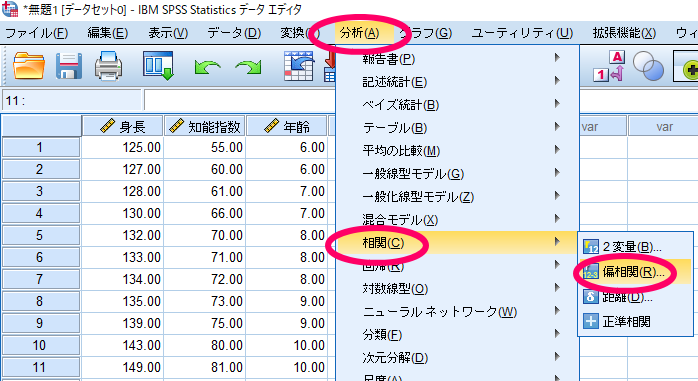
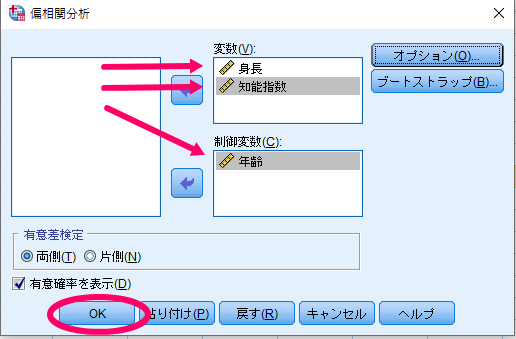
SPSSを使用した偏相関分析の結果の見方・確認方法

これが偏相関分析の結果です.
偏相関分析の結果を見る際にははじめに必ず有意確率を確認しましょう.
有意確率(p)<0.05:相関がある
有意確率(p)≧0.05:相関がない(厳密にいえばあるともないとも言えない)
この場合には,有意確率が0.378で5%以上ですので,年齢を考慮すると身長と知能指数には有意な相関がない(厳密にはあるともないとも言えない)といった解釈ができます.
有意確率が有意水準未満(ここでは5%)であれば,合わせて相関係数(r)を確認します.
この場合には有意確率が5%以上ですので,相関係数は大きな意味を持ちません.
ちなみに偏相関分析の場合にも,相関係数の大きさは以下のような解釈が一般的です.
あくまで目安であって絶対的なものではない点にも注意が必要です.
|r|=1.0~0.7
強い相関がある
|r|=0.7~0.4
中等度の相関がある
|r|=0.4~0.2
弱い相関がある
|r|≦0.2
ほとんどなし
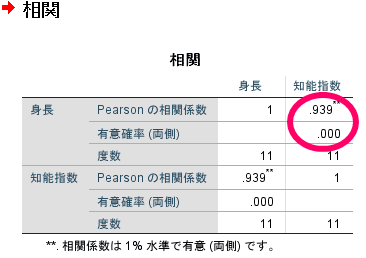
年齢の影響を考慮せずに身長と知能指数の関係を見てみると,p=0.00,r=0.939と有意な強い相関関係が見られます.
偏相関分析では身長と知能指数には有意な相関は認められませんでしたので,年齢が介在する影響力が非常に大きいことがわかります.



コメント