- カイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)と カイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)の違い
- カイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)の適用条件
- SPSSを使用したカイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)-データ入力の方法-
- SPSSを使用したカイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)の方法
- SPSSを使用したカイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)の結果の見方
- SPSSを使用したカイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)の結果の見方 残差分析の重要性
- SPSSを使用したカイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)における効果量の算出
- カイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)の適用条件
- SPSSを使用したカイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)-データ入力の方法-
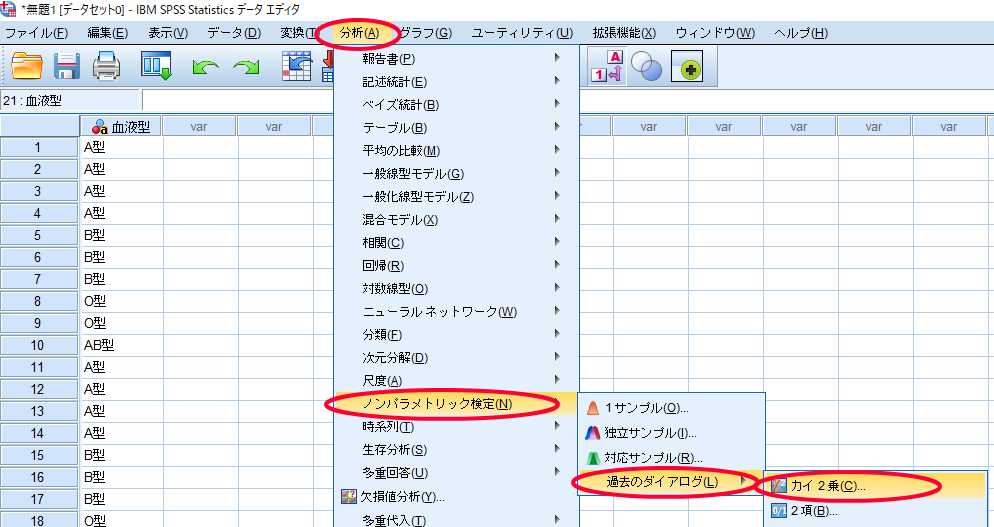
- SPSSを使用したカイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)の方法
- SPSSを使用したカイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)の結果の見方
カイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)と カイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)の違い
測定した変数が名義尺度データ(性別等の数値にならないデータ)の場合には,t検定や相関係数を用いることができません.
名義尺度データの場合には,カイ2乗検定(χ2検定・カイニ乗検定)が用いられます.
カイ2乗検定(χ2検定・カイニ乗検定)には,カイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)とカイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)の2種類が存在します.

カイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)とカイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)ってどう使い分けるの?

カイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)は性別によって試験の合否に差があるかを検討するような場合に使用するのに対して,カイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)はある集団の男性が多いのか少ないのか(比較対象は無い)を検討するような場合に用いられます.
カイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)の適用条件
・名義尺度のデータであること
・順序尺度のデータで段階数が少ないデータであること
SPSSを使用したカイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)-データ入力の方法-
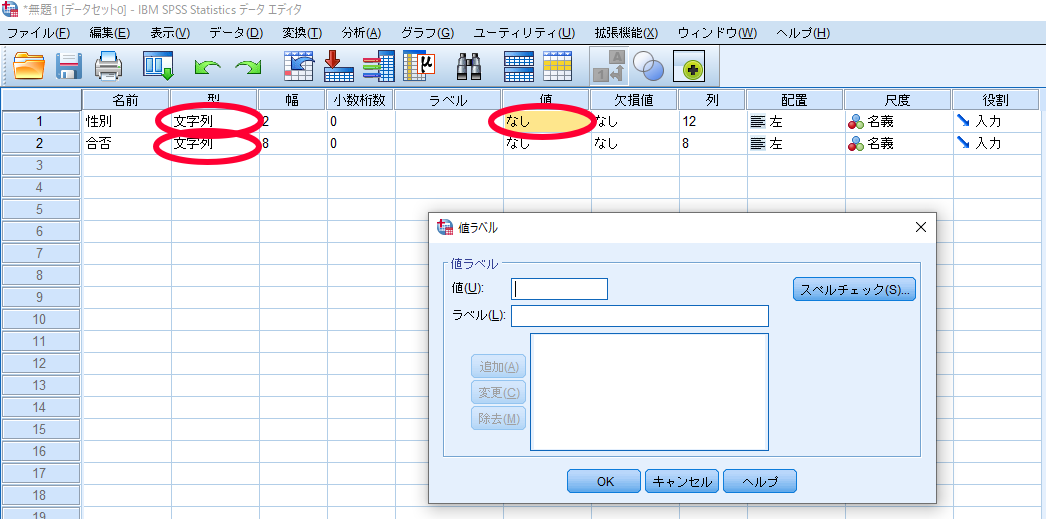
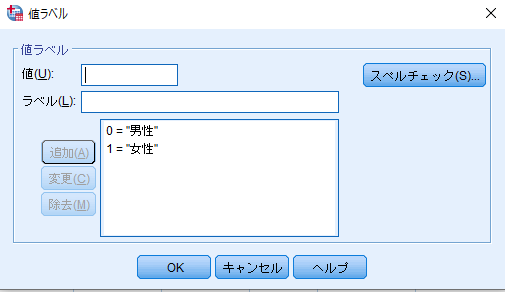
値に「1」,ラベルに「女性」と入力して追加
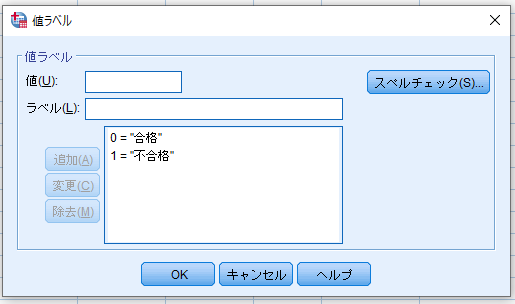
(同様に合否の値も「0=合格」,「1=不合格」となるように入力)


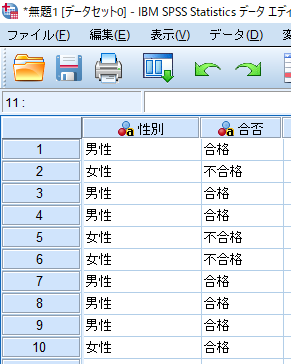
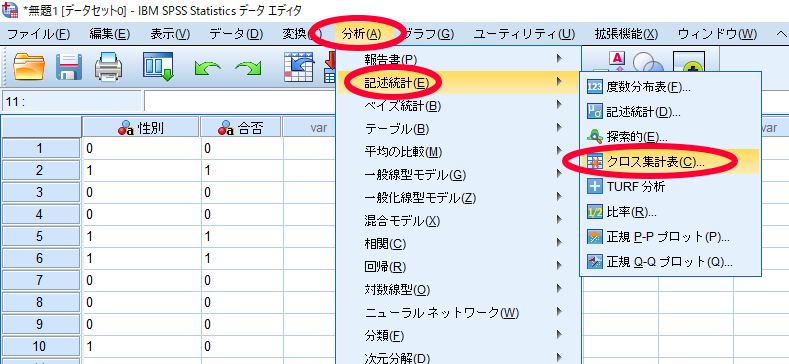
SPSSを使用したカイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)の方法
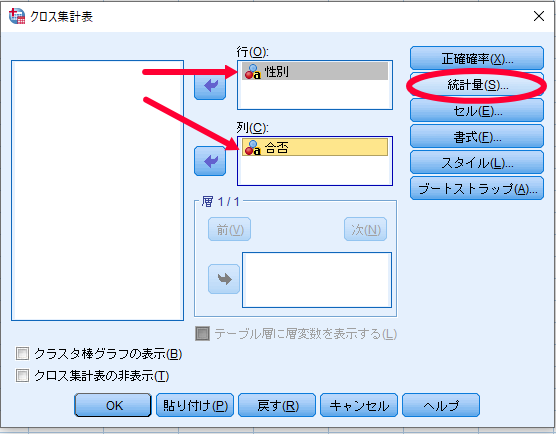
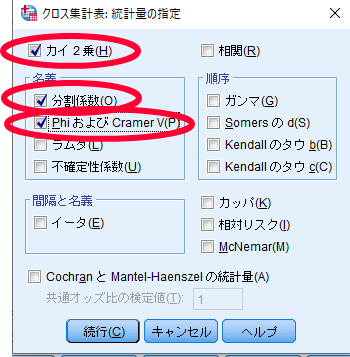
SPSSを使用したカイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)の結果の見方
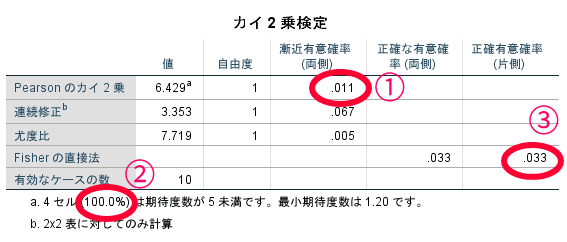
有意確率(p)<0.05:差がある
有意確率(p)≧0.05:差がない(厳密にいえばあるともないとも言えない)

ここで重要なポイントがあります.場合によってはカイ2乗の有意確率ではなく,Fisher(フィッシャー)の直接法の有意確率を参照する必要があります.

どんな時にFisher(フィッシャー)の直接法の有意確率を参照する必要があるの?
SPSSを使用したカイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)の結果の見方 残差分析の重要性

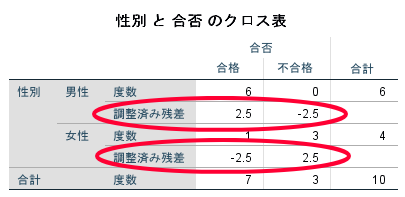
男性の合格者が多いとか,女性の不合格者が多いといった結論を出すにはどうしたらよいの?

男性の合格者が多いとか,女性の不合格者が多いといった結論を出すためには,調整済み残差を参照することが勧められます.
SPSSを使用したカイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)における効果量の算出
最近は検定を行った場合には,有意確率と合わせて効果量を算出するのが一般的になってきております.
t検定やMann-WhitneyのU検定などではSPSSでは効果量を算出することはできませんが,カイ2乗独立性検定の場合には,効果量を算出することが可能です.

ところで効果量って何?

効果量というのはデータの単位に依存しない標準化された効果の程度を表す指標です.
カイ2乗独立性検定の場合には,連関係数(Φ)を参照します.
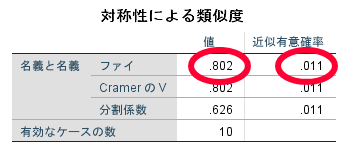

効果量の大きさってどうやって判断するの?

あくまで目安ですが下の表が非常に参考になります.2×2のカイ2乗検定の場合には,連関係数(Φ:ファイ)を,2×3等の2×2以外の場合には連関係数(クラメールのV)を参照します.ここでは2×2ですので連関係数(Φ:ファイ)を参照します.
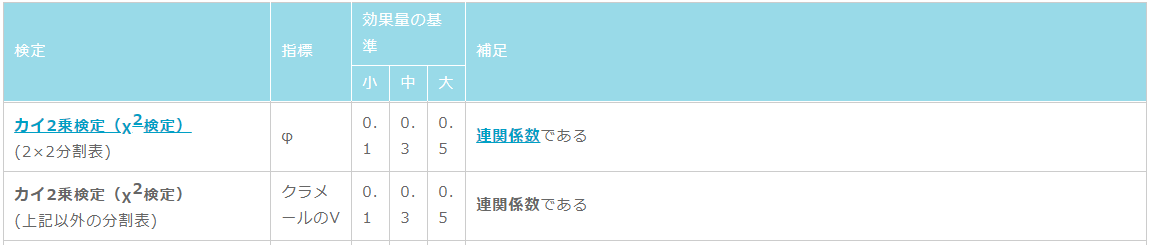
http://jspt.japanpt.or.jp/ebpt_glossary/effect-size.htmlより引用
カイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)の適用条件
冒頭でも述べましたが,カイ2乗独立性検定(χ2独立性検定・カイニ乗独立性検定)は性別によって試験の合否に差があるかを検討するような場合に使用するのに対して,カイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)はある集団の男性が多いのか少ないのか(比較対象は無い)を検討するような場合に用いられます.
・名義尺度のデータであること
・順序尺度のデータで段階数が少ないデータであること
SPSSを使用したカイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)-データ入力の方法-
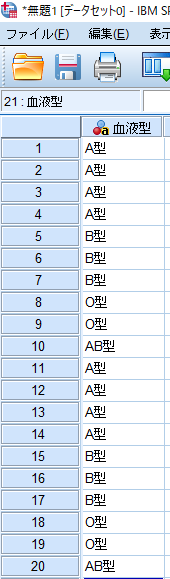
SPSSを使用したカイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)の方法
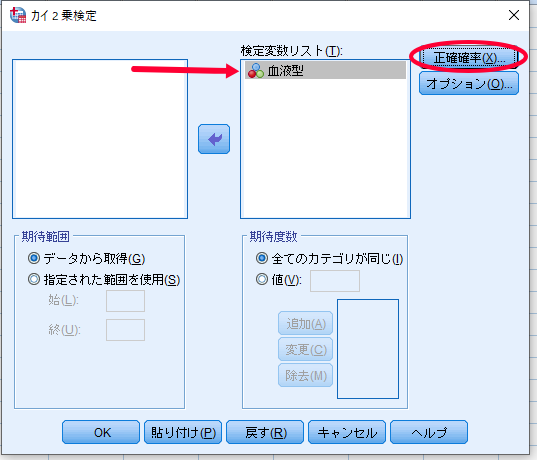

SPSSを使用したカイ2乗適合度検定(χ2適合度検定・カイニ乗適合度検定)の結果の見方
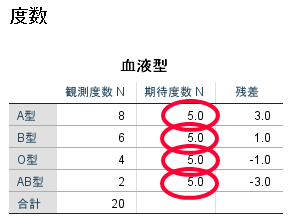
まずは度数を確認しましょう.
カイ2乗適合度検定では,あらかじめ「A型・B型・O型・AB型」といった4種類の血液型が,1:1:1:1の割合になることを想定しており,この1:1:1:1と比較してこの集団の血液型の分布に偏りがあるかどうかを分析したものとなります.
この場合にも20例の対象者を1:1:1:1の割合で分類したものが期待度数の5:5:5:5の部分です.
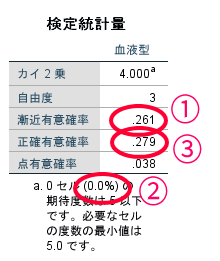
これが最終的なカイ2乗適合度検定の結果です.
基本的には①のカイ2乗の有意確率を確認します.
カイ2乗独立性検定と同様に②が20.0%以上であればfisher(フィッシャー)の正確確率検定の有意確率である③を参照します.
この場合には②が20.0%未満ですので①を参照します.
この場合p=0.261で有意確率が5%以上ですので,この集団の血液型に有意な偏りは無いといった結論(特筆してどの血液型が多いといった結論は出せない)を導くことができます.
仮に血液型の一般的な割合(A型:B型:O型:AB型=4:3:2:1)に比較して今回の集団における血液型の分布に偏りがあるかを検討したいような場合には,下図のように期待度数の値を追加することもできます.
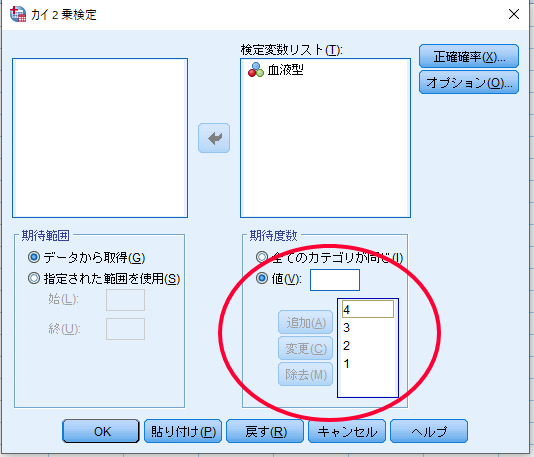
このように割合を変えると期待度数も割合に合わせて変化します.





コメント
[…] […]