- Kruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)の適用の条件
- SPSSを使用したKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)-データの並べ方に注意-
- SPSSを使用した一元配置分散分析の方法
- SPSSによるKruskal-Wallis検定では事後検定であるSteel-Dwass検定が行えない
- SPSSを使用したKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)の結果の見方・確認方法
- SPSSを用いてSPSSを用いたKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)を行った際のグラフ作成
- SPSSを用いたKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)における効果量の算出
Kruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)の適用の条件
Kruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)を適用するためにはいくつかの条件を満たす必要があります.
ここではまずKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)を適用するための4つの条件をお示しいたします.
・正規分布以外に従うデータ(正規性の判断についてはコチラを参照してください)
・データが比率尺度データまたは間隔尺度データ
(例外として多段階の順序度データでも使用することあります)
・中央値を比較することが意味を持つデータ
・対応がない3つ以上の標本を対象としたデータ
(2つの標本を対象としたデータの場合にはMann-WhitneyのU検定を使用します)

対応がないって何?

対応がないというのは比べるデータが同一対象例のデータではないことを意味します
ここで重要なのはKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)というのは3つ以上の標本に対して用いられる検定であるといった点です.
例えば若年者と前期高齢者と後期高齢者で握力を比較するとか,大学生と高校生と中学生で体重を比較するといったような場合には,異なる対象例のデータを比較することとなります.
このように異なる対象例の3つ以上のノンパラメトリックの分布に従うデータを比較する場合にはKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)を用いることとなります.
SPSSを使用したKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)-データの並べ方に注意-
SPSSでKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)を行う場合にはデータの並べ方にも注意が必要です.
実は対応のある検定と対応の無い検定ではデータの並べ方も異なります.
3群以上の差の検定で用いられるノンパラメトリック検定には,Kruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)(対応のない検定)とFriedman検定(フリードマン検定)(対応のある検定)といった手法がありますが,Kruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)とFriedman検定(フリードマン検定)ではデータの並べ方も異なるものとなりますので,注意が必要です.
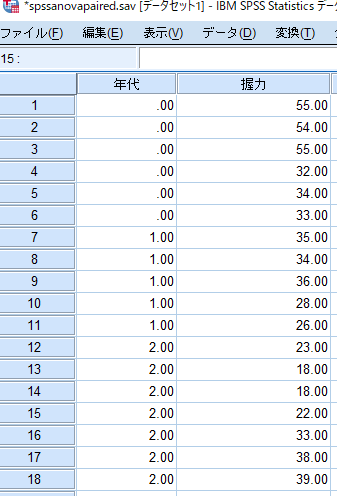
一元配置分散分析の場合には,測定データ(握力)を縦列に並べ,その横にグループを表すデータ(年代:若年者=0,前期高齢者=1,後期高齢者=2)を入力します.
SPSSにデータを移行する前にエクセルでデータベースを作成することが多いと思いますが,エクセルでデータ整理をする段階でこのようなデータのまとめ方をしておくと,エクセルからSPSSへのデータ移行が容易となります.
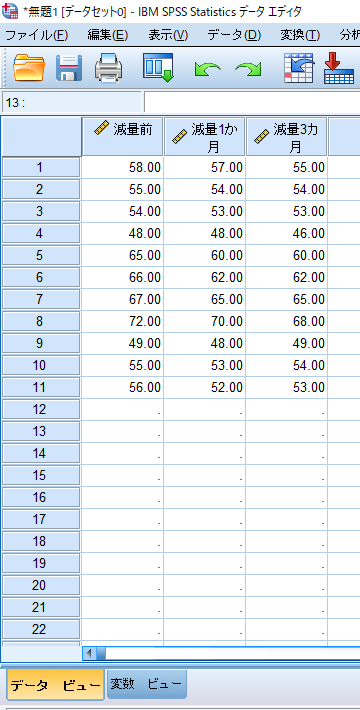
ちなみにFriedman検定の場合にはこんな感じです.
対応のある検定の場合には,このように横列に同一対象者のデータを並べます.
SPSSを使用した一元配置分散分析の方法
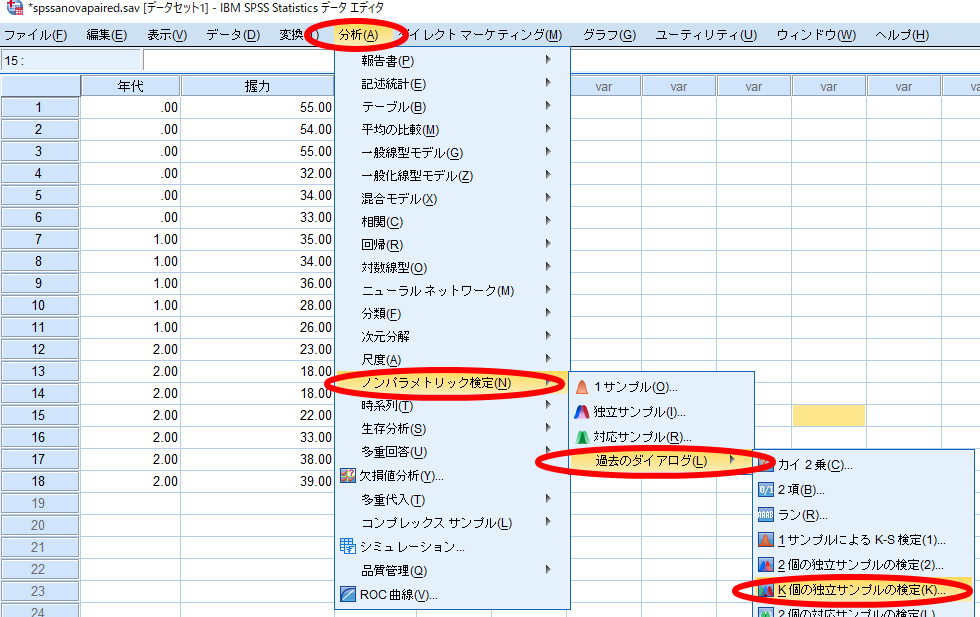
年代(若年者=0,前期高齢者=1,後期高齢者=2)毎に握力を比較する例をお示ししながら話を進めていきます.
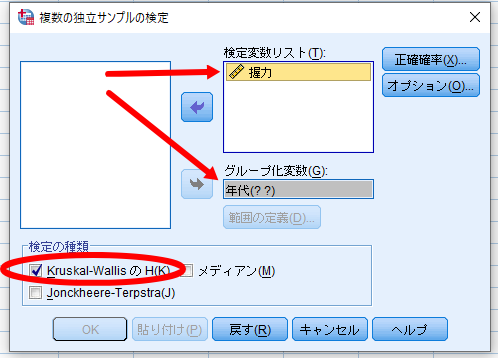
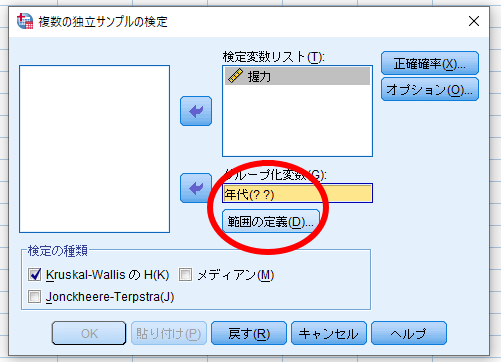
年代(??)をクリックすると,範囲の定義の表示が反転されるので,範囲の定義をクリック
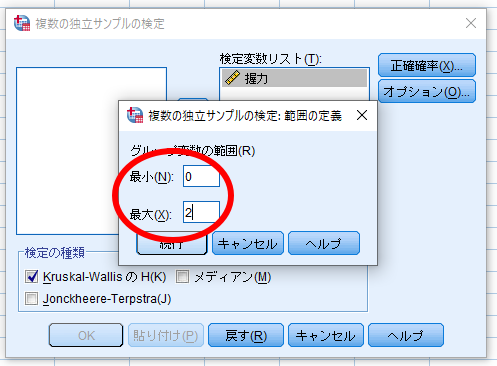
ここでは0=若年者,1=前期高齢者,2=後期高齢者としておりますので,最小値は0,最大値は2を入力します.
その後に続行をクリックします.
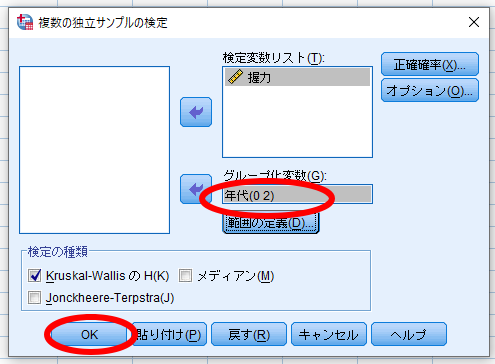
グループ化変数が年代(0 2)と表記されていることを確認して,OKをクリックします.
SPSSによるKruskal-Wallis検定では事後検定であるSteel-Dwass検定が行えない
一元配置分散分析では事後検定(多重比較法)を選択して,その後の検定の設定を行いましたが,SPSSによるKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)では多重比較法であるSteel-Dwass検定を行うことができません.
3群以上の差の検定では,多重比較法と呼ばれる検定手法を用いて,Kruskal-Wallis検定による結果が有意であった場合に,1つ1つの水準(ここでは若年者・前期高齢者・後期高齢者)の間のどこに有意な差があるのかを明らかにする流れが一般的です(実はKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)を行うことなくSteel-Dwass法を適応しても間違いではありませんが慣習的にKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)を行って,結果が有意であった場合に多重比較法であるSteel-Dwass法を用いるのが一般的です).
Kruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)が有意であった場合には,水準(ここでは若年者・前期高齢者・後期高齢者)間のどこかに差があることはわかりますが,どこに差があるかまではわかりませんので,どことどこに差があるかを多重比較法(Steel-Dwass法)を用いて明らかにするわけです.
残念ながらSPSSにはSteel-Dwass法が搭載されておりませんので,別の統計ソフト(R等)を用いて,Steel-Dwass検定を行うかBonferroni法やHolm法を用いて多重比較を行うのが一般的です.
Bonferroni法やHolm法についてはまた今度解説させていただきます.
SPSSを使用したKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)の結果の見方・確認方法
Kruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)の結果を確認する方法は簡単です.
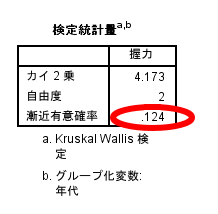
これがKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)の結果です.
Kruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)の結果を読み取る際には以下のように判断します.
有意確率(p)<0.05:3群のどこかに差がある
有意確率(p)≧0.05:3群のどこにも差がない(厳密にいえばあるともないとも言えない)
この場合には,有意確率(p値)=0.124≧0.05となっておりますので,若年者・前期高齢者・後期高齢者の握力のデータには差がない(差があるともないとも言えない)と判断できます.
SPSSを用いてSPSSを用いたKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)を行った際のグラフ作成
SPSSを用いたKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)を用いる場合にはデータに正規性が確認できないことが前提となりますので,SPSSを用いたKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)を用いた場合に使用すべきグラフは中央値と四分位を用いた箱ひげ図です.
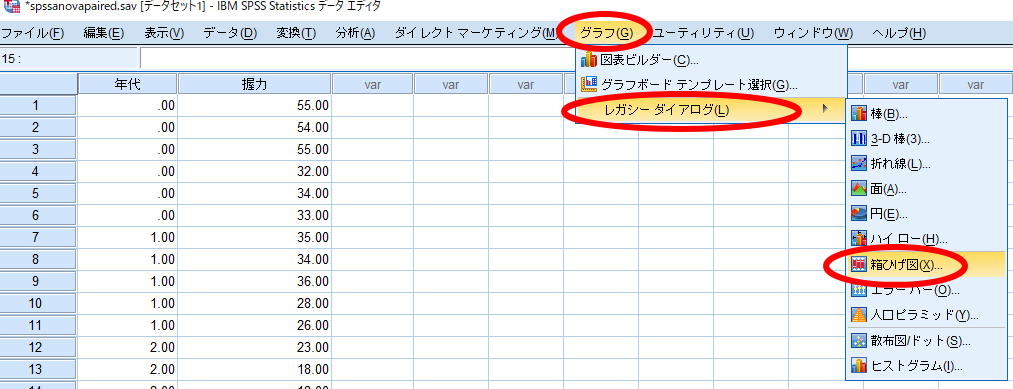
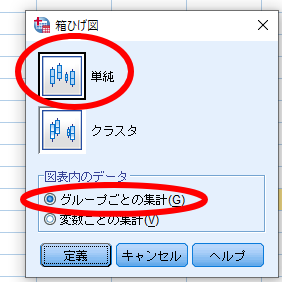
ここで重要なのはKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)のような対応のないデータの場合には,図表内のデータで「グループごとの集計」を選択する点です.
ちなみに対応のあるデータを用いてエラーバーグラフを作成する場合には,図表内のデータで「変数ごとの集計」を選択する必要があります.
最後に「定義」をクリックします.
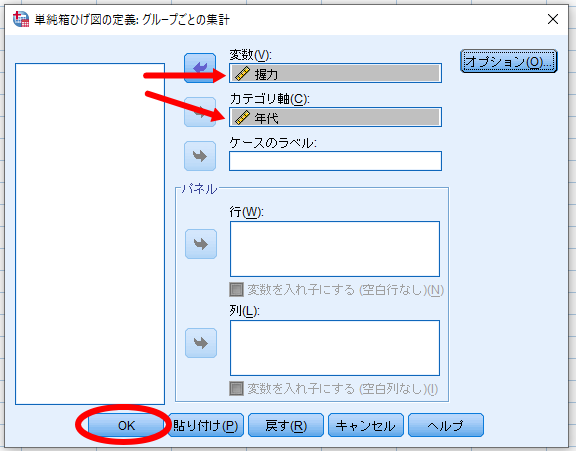
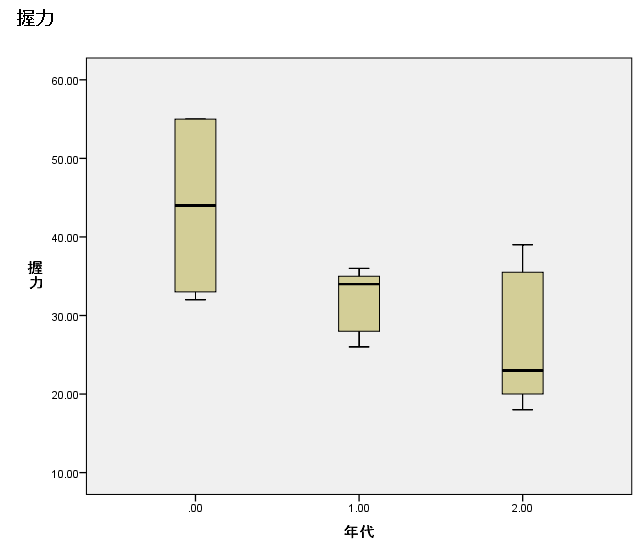
これが完成した箱ひげ図です.
箱の中央の横線が中央値,箱の上側が第3四分位,箱の下側が第1四分位を表します.
ちなみにひげの部分は上側は外れ値を除いた最大値,下側は外れ値を除いた最小値となります.
SPSSを用いたKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)における効果量の算出
最近はKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)を行った場合には,有意確率と合わせて効果量を算出するのが一般的になってきております.
しかしながらKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定)では,効果量の算出が難しく,提示の意味もあまりないことから,多重比較として行うMann-Whitney(マン・ホイットニー)のU検定のみの効果量を提示するのが一般的です.

ところで効果量って何?

効果量というのはデータの単位に依存しない標準化された効果の程度を表す指標です.
先ほど若年者・前期高齢者・後期高齢者における握力差の大きさについて検討いたしました.
例えばある研究では筋力差を握力計を用いて検討を行っていたのに対して,ある研究では筋力差を背筋力を用いて検討を行っていたとします.
この場合にはアウトカムの単位が異なりますので2つの研究の間でどちらが筋力差が大きいのかを単純比較することができません.
このように単位の異なる研究から得られた効果の比較や人数の異なる研究から得られた効果を比較する際に役立つのが効果量という指標です.
前述したようにKruskal-Wallis検定(クラスカルワリス検定・クラスカルウォリス検定),多重比較として行うMann-Whitney(マン・ホイットニー)のU検定の効果量を提示します.
Mann-Whitney(マン・ホイットニー)のU検定の効果量の算出方法については以下をご参照ください.






コメント
教えていただきたいのですが、マンホイットニー検定や、クラスカルウォリス検定は、中央値に差があるかを検定していると思いますが、作表するときには、何を記せばいいでしょうか。
平均値と標準偏差が書かれている表は、よく見かけますが、解説書のようなものには、ノンパラのときは平均値や標準偏差は意味を持たないとも書かれています。
では、結果はどのように表で表せばよいのでしょうか。
度数とパーセントを書く方法もあると思いますが、クラスカルウォリス検定の結果、度数とパーセントで作表されているものは、あまり見かけません。
平均値と標準偏差を表す表記方法は、間違っているといえるのでしょうか。
あるいは「本来中央値と四分位範囲を表すべきだけれども、便宜上、平均値と標準偏差を記入することもある」という解釈であってますか?
こちらからご相談いただければ対応させていただきます。
ご検討よろしくお願いいたします.
https://coconala.com/services/1298587?ref=top_histories&ref_kind=home&ref_no=2