SPSSによるFriedman検定(フリードマン検定)の適用の条件
SPSSを用いたFriedman検定(フリードマン検定)を適用するためにはいくつかの条件を満たす必要があります.
ここではまずFriedman検定(フリードマン検定)を適用するための4つの条件をお示しいたします.
・正規分布に従わないデータ(正規性の判断についてはコチラを参照してください)
・データが比率尺度データまたは間隔尺度データ
(例外として多段階の順序度データでも使用することあります)
・中央値を比較することが意味を持つデータ
・1つの標本に対して3つ以上の条件を変えて,反復測定したノンパラメトリックデータ
(1つの標本に対して2つの条件を変えて反復測定したノンパラメトリックデータの場合にはWilcoxonの符号付順位和検定を使用します)

反復測定によるって何?

反復測定によるというのは比べるデータが同一対象例のデータであることを意味します
ここで重要なのはFriedman検定(フリードマン検定)というのは1つの標本に対して3つ以上の条件を変えて反復測定したデータに用いられる検定であるといった点です.
例えばダイエットを行った場合に,ダイエット開始前・ダイエット開始1か月後・ダイエット開始3か月後で体重を比較するとか,体組成率の日差変動をみるために朝・昼・夜に体組成率を測定して比較するいったような場合には,同一対象例の3条件のデータを比較することとなります.
このように同一対象例を対象として3条件以上のデータを比較する場合にはFriedman検定(フリードマン検定)を用いることとなります.
ちなみに対応のない3条件以上の比較にはデータに正規性が確認できなければ,Kruskal-Wallis検定(クラスカル・ワリス検定,クラスカル・ウォリス検定)を用いることとなります.
SPSSを使用したFriedman検定(フリードマン検定)-データの並べ方に注意-
SPSSでFriedman検定(フリードマン検定)を行う場合にはデータの並べ方にも注意が必要です.
実は反復測定による(対応のある検定)と対応の無い検定ではデータの並べ方も異なります.
3群以上の差の検定で用いられるノンパラメトリック検定には,Kruskal-Wallis検定(クラスカル・ワリス検定,クラスカル・ウォリス検定)(対応のない検定)とFriedman検定(フリードマン検定)(反復測定による検定,対応のある検定)といった手法がありますが,Kruskal-Wallis検定(クラスカル・ワリス検定,クラスカル・ウォリス検定)とFriedman検定(フリードマン検定)ではデータの並べ方も異なるものとなりますので,注意が必要です.
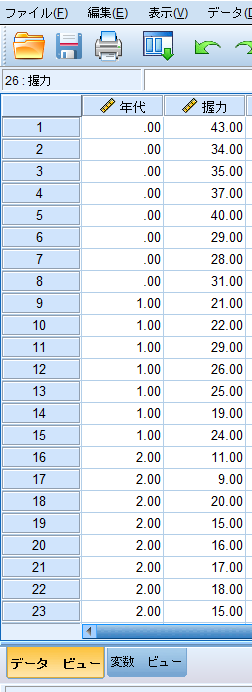
Kruskal-Wallis検定(クラスカル・ワリス検定,クラスカル・ウォリス検定)の場合には,測定データ(体重)を縦列に並べ,その横にグループを表すデータ(年代:若年者=0,前期高齢者=1,後期高齢者=2)を入力します.
SPSSにデータを移行する前にエクセルでデータベースを作成することが多いと思いますが,エクセルでデータ整理をする段階でこのようなデータのまとめ方をしておくと,エクセルからSPSSへのデータ移行が容易となります.
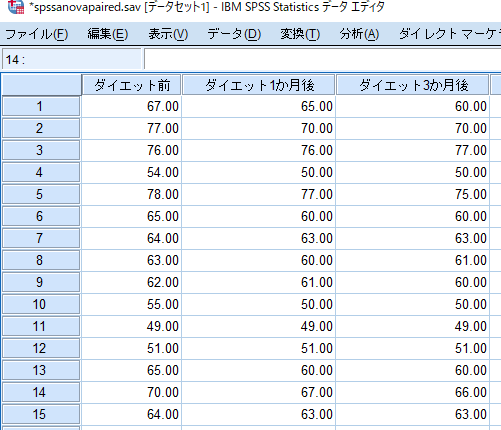
ちなみにFriedman検定(フリードマン検定)の場合にはこんな感じです.
反復測定による検定(対応のある検定)の場合には,このように横列に同一対象者のデータを並べます.
SPSSにデータを移行する前にエクセルでデータベースを作成することが多いと思いますが,エクセルでデータ整理をする段階でこのようなデータのまとめ方をしておくと,エクセルからSPSSへのデータ移行が容易となります.
SPSSを使用したFriedman検定(フリードマン検定)の方法
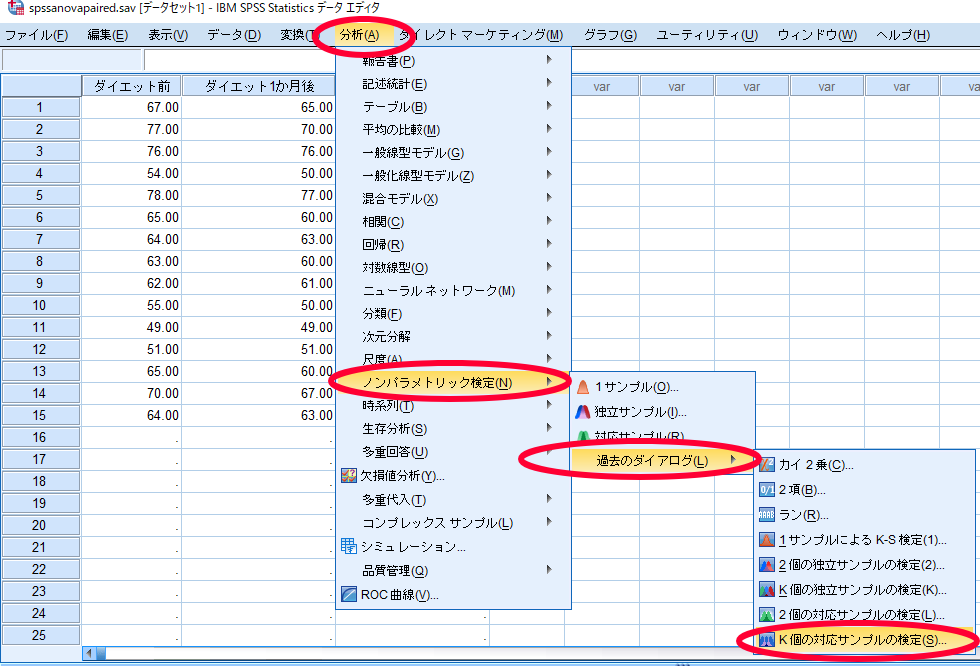
ここではダイエット前・ダイエット1か月後・ダイエット3か月後に体重のデータを比較する例をお示ししながら話を進めていきます.
Friedman検定(フリードマン検定)は非正規分布のデータに用いられる統計手法ですので,事前にShapiro-wilk検定を用いて正規性の検定を行って,3群のうちいずれか1群のデータの分布が正規分布でないことを確認しておく必要があります.
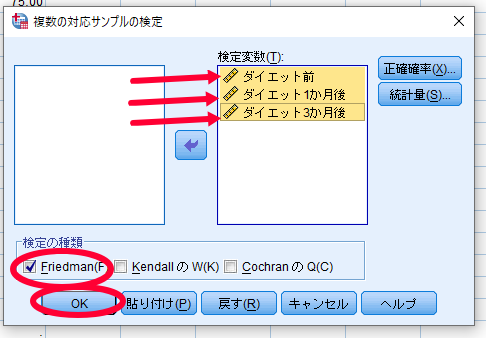
ダイエット前・ダイエット1か月後・ダイエット3か月後を検定変数へ移動させる.
Friedman検定にチェックが入っているのを確認してOKをクリック
SPSSを使用したFriedman検定(フリードマン検定)の結果の見方・確認方法
Friedman検定(フリードマン検定)の結果を確認する際には見るポイントについてご説明いたします.
①有意確率の確認
Friedman検定の結果を確認する際には,漸近有意確率を確認します.

有意確率(p)<0.05:3群のどこかに差がある
有意確率(p)≧0.05:3群のどこにも差がない(厳密にいえばあるともないとも言えない)
この場合には,有意確率が0.00<0.05となっておりますので,ダイエット前・ダイエット1か月後・ダイエット3か月後の3群の間のどこかに差があると解釈できます.
ただここまでの結果からは具体的にどことどこに差があるのかはわかりません.
SPSSによるFriedman検定では事後検定であるBonferroni検定が行えない
反復測定による一元配置分散分析では事後検定(多重比較法)を選択して,その後の検定の設定を行いましたが,SPSSによるFriedman検定(フリードマン検定)では多重比較法であるBonferroni法を適用することができません.
3群以上の差の検定では,多重比較法と呼ばれる検定手法を用いて,Friedman検定(フリードマン検定)による結果が有意であった場合に,1つ1つの水準(ここではダイエット前・ダイエット1か月後・ダイエット3か月後)の間のどこに有意な差があるのかを明らかにする流れが一般的です(実はFriedman検定(フリードマン検定)を行うことなくBonferroni法を適応しても間違いではありませんが慣習的にFriedman検定(フリードマン検定)を行って,結果が有意であった場合に多重比較法であるBonferroni法を用いるのが一般的です).
Friedman検定(フリードマン検定)が有意であった場合には,水準(ここではダイエット前・ダイエット1か月後・ダイエット3か月後)間のどこかに差があることはわかりますが,どこに差があるかまではわかりませんので,どことどこに差があるかを多重比較法(Bonferroni法)を用いて明らかにするわけです.
残念ながらSPSSにはBonferroni法が搭載されておりませんので,別の統計ソフト(R等)を用いて,Bonferroni法やHolm法を用いて多重比較を行うのが一般的です.
Bonferroni法やHolm法についてはまた今度解説させていただきます.
SPSSを用いてFriedman検定(フリードマン検定)を行った際のグラフ作成
SPSSを用いたFriedman検定(フリードマン検定)を用いる場合にはデータに正規性が確認できないことが前提となりますので,SPSSを用いたFriedman検定(フリードマン検定)を用いた場合に使用すべきグラフは中央値と四分位を用いた箱ひげ図です.
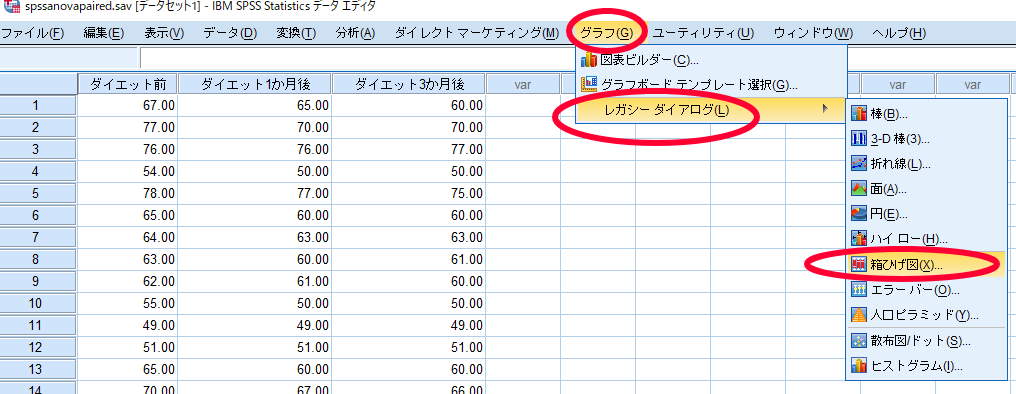
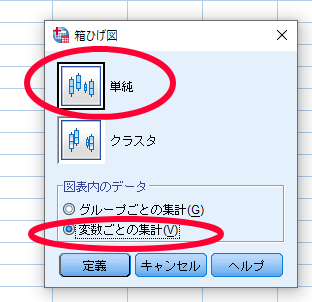
ここで重要なのは反復測定によるデータ(対応のあるデータ)の場合には,図表内のデータで「変数ごとの集計」を選択する点です.
ちなみに対応のないデータを用いて箱ひげ図を作成する場合には,図表内のデータで「グループごとの集計」を選択する必要があります.
最後に「定義」をクリックします.
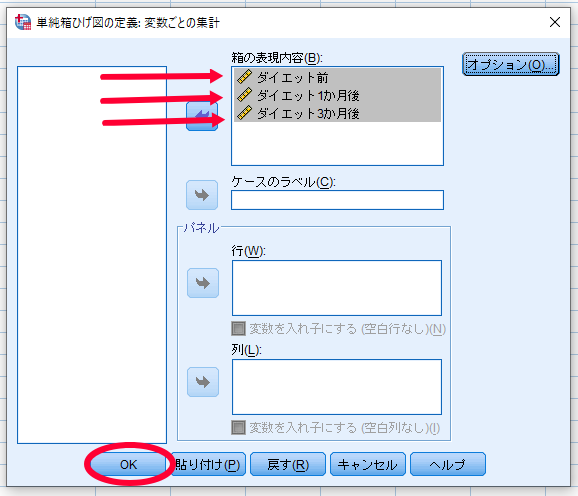
ダイエット前・ダイエット1か月後・ダイエット3か月後を箱の表現内容へ移動させます.
移動させたのちにOKをクリックします.
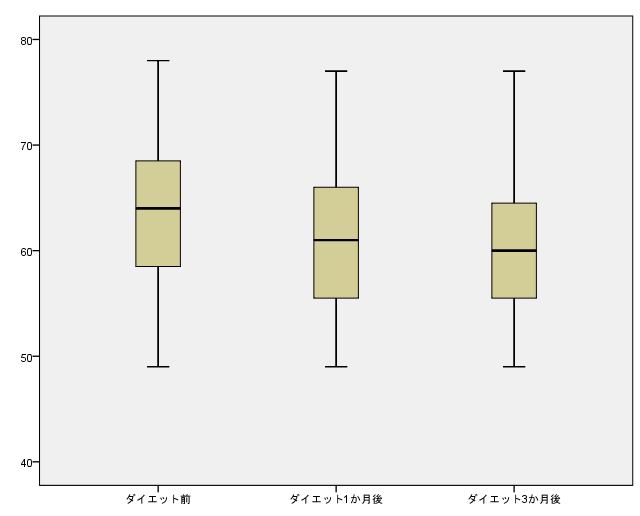
これが完成した箱ひげ図です.
中央の横線が中央値,箱の上側が第3四分位,箱の下側が第1四分位,ひげの上側が外れ値を除いた最大値,ひげの下側が外れ値を除いた最小値をを表します.
SPSSを用いたFriedman検定(フリードマン検定)における効果量の算出
最近はFriedman検定(フリードマン検定)を行った場合には,有意確率と合わせて効果量を算出するのが一般的になってきております.
しかしながらFriedman検定(フリードマン検定)では,効果量の算出が難しく,提示の意味もあまりないことから,多重比較として行うWilcoxonの符号付順位和検定のみの効果量を提示するのが一般的です.

ところで効果量って何?

効果量というのはデータの単位に依存しない標準化された効果の程度を表す指標です.
単位の異なる研究から得られた効果の比較や人数の異なる研究から得られた効果を比較する際に役立つのが効果量という指標です.
前述したようにFriedman検定(フリードマン検定)の場合には,多重比較として行うWilcoxonの符号付順位和検定の効果量を提示します.
Wilcoxonの符号付順位和検定の効果量の算出方法については以下をご参照ください.






コメント