SPSSを用いた対応のないt検定（2標本t検定）　95%信頼区間・エラーバーグラフ・効果量

対応のないt検定（2標本t検定）の適用の条件

対応のないt検定（2標本t検定）を適用するためにはいくつかの条件を満たす必要があります．

ここではまず対応のないt検定（2標本t検定）を適用するための4つの条件をお示しいたします．

 

ここで重要なのは対応のないt検定（2標本t検定）というのは2つの標本に対して用いられる検定であるといった点です．

例えば男性と女性で体重を比較するとか，高齢者と若年者で握力を比較するといったような場合には，異なる対象例のデータを比較することとなります．

このように異なる対象例の2つのデータを比較する場合には対応のないt検定（2標本検定）を用いることとなります．

 

 

 

 

 

 

 

 

 

 

SPSSを使用した対応のないt検定（2標本t検定）-データの並べ方に注意-

SPSSでt検定を行う場合にはデータの並べ方にも注意が必要です．

実は対応のある検定と対応の無い検定ではデータの並べ方も異なります．

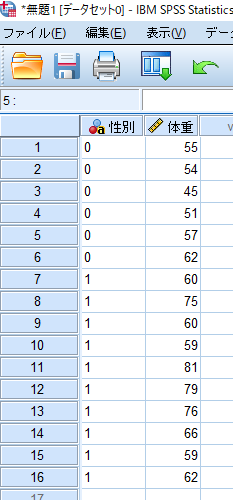
対応の無い検定の場合には，測定データ（体重）を縦列に並べ，その横にグループを表すデータ（性別等：女性=0，男性=1）を入力します．

SPSSにデータを移行する前にエクセルでデータベースを作成することが多いと思いますが，エクセルでデータ整理をする段階でこのようなデータのまとめ方をしておくと，エクセルからSPSSへのデータ移行が容易となります．

 

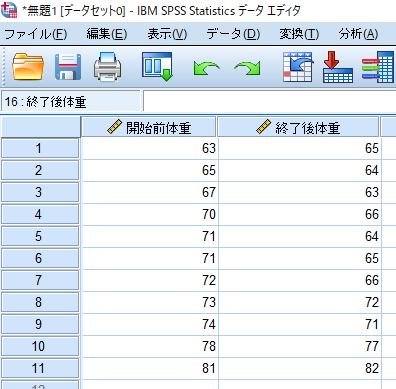
対応のある検定の場合には，このように横列に同一対象者のデータ（ダイエット前後での体重）を並べます．

 

 

 

 

 

 

 

 

 

 

 

 

 

SPSSを使用した対応のないt検定（2標本t検定）の方法

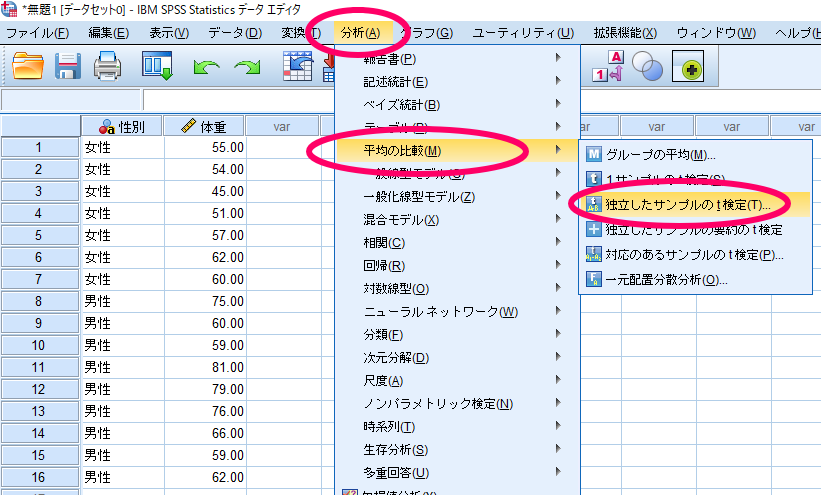
ここでは男性と女性の体重を比較することを想定して話を進めます．

 

 

 

 

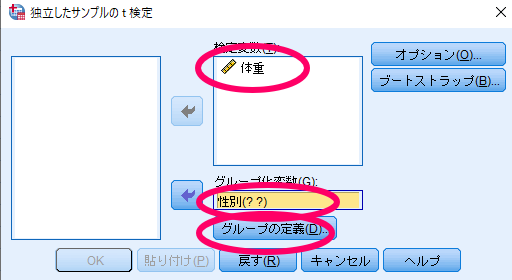
ここでグループ化変数が「性別（？？）」といった表記になっていることを確認して，グループの定義をクリックします．

 

 

 

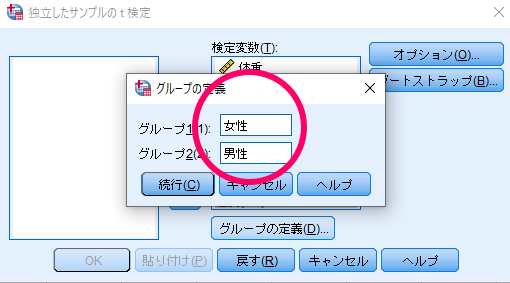
ここでグループ1・グループ2の属性を入力しておきます．

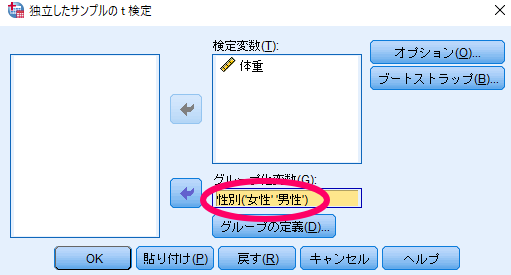
うまく入力できればグループ化変数が「性別（？？）」から「性別（’女性’’男性’）」と表記に変わります．

ちなみに変数ビューで性別の「型」を「文字列」に，「尺度」を「名義」にしておかないとグループの定義ができませんので注意が必要です．

95%信頼区間を算出する場合にはオプションは操作する必要はありません．

信頼区間を99%に修正したいといったような場合には，オプションから信頼区間を修正する必要があります．

 

 

 

 

 

 

 

 

 

 

 

SPSSを使用した対応のないt検定（2標本t検定）の結果の見方・確認方法

これが対応のないt検定（2標本t検定）の結果です．

対応のないt検定（2標本t検定）を結果を確認する際には見るポイントが6つあります．

①平均値

男性と女性それぞれの体重の平均値がそれぞれ出力されておりますので，まずは平均値を確認しましょう．

平均値と合わせて算出されている標準偏差も確認しましょう．

平均値と標準偏差を見れば，集団のデータがどの範囲にあるのかがおおよそ把握できます．

 

対応のないt検定と対応のあるt検定の大きな相違はこの部分です．

実は対応のないt検定（2標本t検定）ではt検定を行う前に，等分散性の検定を行う必要があります．

基本的にはLeveneの検定における有意確率に応じて出力の参照する部分が異なります

今回のデータでは，Levene検定の結果，有意確率が0.024と出力されております．

したがって不等分散と判断できますので，下の列の有意確率や95%信頼区間を参照する必要があります．

 

この有意確率を見れば，男性と女性の間の体重に差があるのかどうかがわかります．

この場合には，有意確率が0.03で5%未満ですので，男性と女性の間の体重で有意な差があるといった解釈ができます．

差の95%信頼区間を確認すると，下限が-21.7kg，上限が-5.68と出力されているのがわかります．

この場合で言うとダイエット前後での体重の変化は，95%の確率で-21.7kg～-5.68の間にあるという解釈になります．

つまり男女間の体重の差は20kgを超える場合もあるし，5.0kg程度である可能性もあると解釈できます．

ここで重要なのは今回は差の95%信頼区間が0をまたいでいない（この場合，上限値が正の値になっていない）という点です．

有意確率が5%以上となっている場合には，95%信頼区間が0をまたぐ（この場合，上限値が正の値になる）ようになります．

さらにこの95%信頼区間の大きさを確認することで，差がどのくらい意味のあるものかを判断することができます．

例えば有意確率が5%未満であっても，差の95%信頼区間が0.1～0.2であったのであれば，そんな差はあまり意味のない差としてとらえることができるでしょう．

今回のデータでは有意確率が5%未満で，かつ差の95%信頼区間が-20kg～-5kgですから男女間での体重差は非常に大きいと判断できるでしょう．

この自由度やt値というのはいわゆる統計量と呼ばれるものです．

素人が理解しておく必要はあまりないものですが，効果量を算出する上ではこの自由度とt値が必要となります．

効果量についてはまた後でご紹介させていただきますので，ここでは効果量を算出するために必要な数値であるくらいの認識で良いと思います．

 

 

 

 

 

 

 

 

 

 

 

SPSSを用いて対応のないt検定（2標本t検定）を行った際のグラフ作成

対応のないt検定を用いる場合にはデータに正規性が確認できることが前提となりますので，対応のないt検定を用いた場合に使用すべきグラフは平均値と95%信頼区間を用いたエラーバーグラフです．

 

 

 

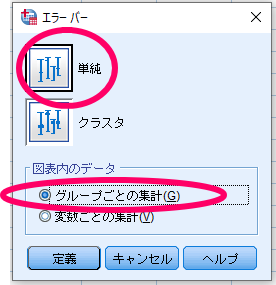
ここで重要なのは対応のないデータの場合には，図表内のデータで「グループごとの集計」を選択する点です．

ちなみに対応のあるデータを用いてエラーバーグラフを作成する場合には，図表内のデータで「変数ごとの集計」を選択する必要があります．

最後に「定義」をクリックします．

 

 

 

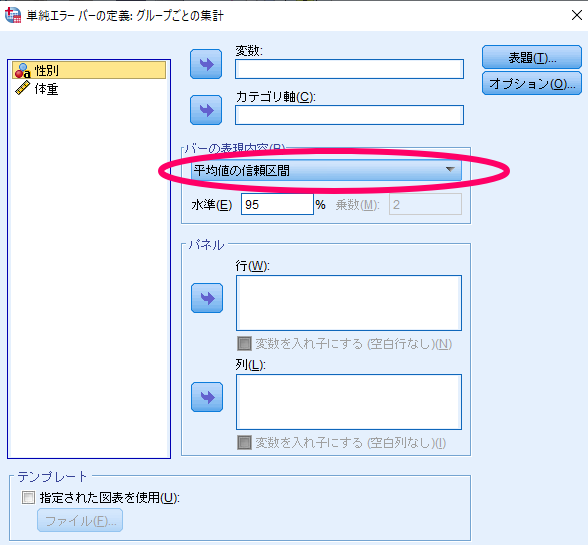
デフォルト設定は平均値の95%信頼区間となっておりますが，標準誤差や標準偏差を用いてグラフを作成することも可能です．

 

 

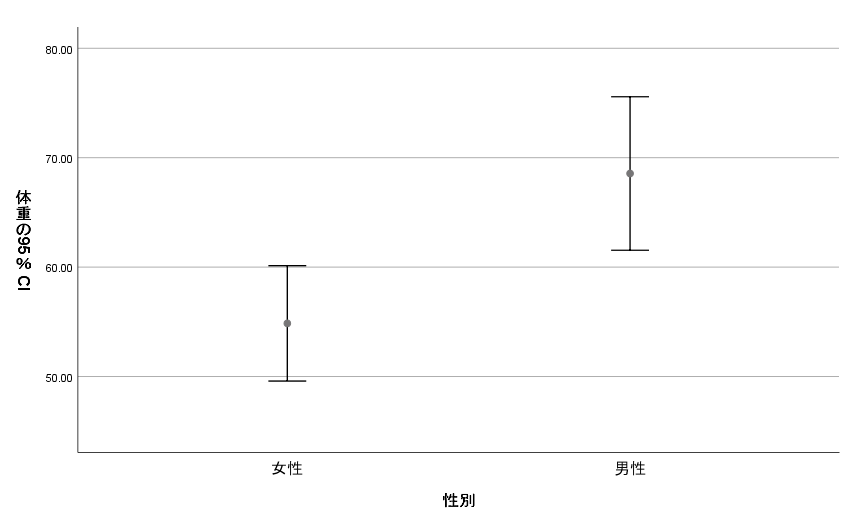
これが完成したエラーバーグラフです．

中央の小さい●印が平均値，上下のバーが95%信頼区間を表しております．

 

 

 

 

 

 

 

 

 

対応のないt検定（2標本t検定）における効果量（r・d）の算出

最近は対応のないt検定（2標本t検定）を行った場合には，有意確率・95%信頼区間と合わせて効果量（rやd）を算出するのが一般的になってきております．

はじめにSPSSでは効果量を算出することはできませんので，先ほどお示しいたしました自由度やt値といった統計量を使用して効果量を算出することになります．

先ほど男女間における体重差の大きさを95%信頼区間を用いて考察いたしました．

例えばある研究では男女間の体格差をアウトカムを体重（kg）を用いて検討を行っていたのに対して，ある研究では男女間の体格差を，BMI（kg/cm2）をアウトカムとして検討を行っていたとします．

この場合にはアウトカムの単位が異なりますので2つの研究の間でどちらが男女間の体格差が大きいのかを単純比較することができません．

このように単位の異なる研究から得られた効果の比較や人数の異なる研究から得られた効果を比較する際に役立つのが効果量という指標です．

特にrという効果量と，dという効果量の2種類が代表的です．

rもdも計算方法が異なるだけで意味は同一なのですが，rは0～1（もしくは0～-1）の範囲をとるので理解しやすく，差の検定ではrが用いられることが多いです．

 

ここではこのエクセルファイルを用いて効果量（r）を算出いたしました．

先ほどのSPSSを用いて行った対応のあるt検定の結果で得られたt値=-3.675と自由度=13.506を上記のエクセルファイルに打ち込むと簡単に効果量が算出できます．

この場合には効果量（r）=0.71で効果量大と判定されました．

つまり差の程度が効果量から見ても大きいという解釈ができます．

 

http://jspt.japanpt.or.jp/ebpt_glossary/effect-size.htmlより引用